



Next: Paura dei ``pregiudizi''? Inevitabilità
Up: Dalla probabilità degli effetti
Previous: Verosimiglianza
Indice
Una volta fissata la funzione di verosimiglianza e un valore osservato
 , si tratta di
costruire la
, si tratta di
costruire la
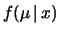 . Per arrivare in modo
euristico alla formula generale, consideriamo soltanto due possibili
valori di
. Per arrivare in modo
euristico alla formula generale, consideriamo soltanto due possibili
valori di 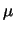 . Se, in base alle nostre conoscenze,
riteniamo i due valori ugualmente probabili,
ci sembrerà naturale protendere per il valore per il quale la
verosimiglianza di osservare
. Se, in base alle nostre conoscenze,
riteniamo i due valori ugualmente probabili,
ci sembrerà naturale protendere per il valore per il quale la
verosimiglianza di osservare  è maggiore. Ad esempio, se
è maggiore. Ad esempio, se
 ,
, 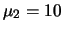 e
e  , si è tentati a credere che
l'osservazione sia dovuta più verosimilmente alla causa
, si è tentati a credere che
l'osservazione sia dovuta più verosimilmente alla causa 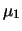 che alla causa
che alla causa 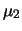 . Se però la grandezza di interesse
è definita positiva, la causa
. Se però la grandezza di interesse
è definita positiva, la causa 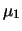 crolla da causa più
probabile a causa impossibile.
Ci sono poi casi intermedi in cui, per motivi
legati all'esperienza precedente, si tende a credere
a priori più
ad una causa che all'altra. Ne segue che il grado di fiducia
risultante di un certo valore di
crolla da causa più
probabile a causa impossibile.
Ci sono poi casi intermedi in cui, per motivi
legati all'esperienza precedente, si tende a credere
a priori più
ad una causa che all'altra. Ne segue che il grado di fiducia
risultante di un certo valore di
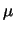 sarà
proporzionale sia alla verosimiglianza
che esso produca il valore osservato che al grado di fiducia
che si attribuiva a
sarà
proporzionale sia alla verosimiglianza
che esso produca il valore osservato che al grado di fiducia
che si attribuiva a 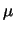 prima
dell'osservazione9.4:
prima
dell'osservazione9.4:
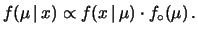 |
(9.4) |
Questo è uno dei modi di scrivere il teorema di Bayes, che ha un
ruolo centrale nelle inferenze probabilistiche.
L'inessenziale fattore di
proporzionalità è ricavato dalla condizione di normalizzazione
(l'integrale su tutti i possibili valori di 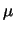 deve dare 1).
deve dare 1).
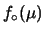 è chiamata distribuzione iniziale, o a priori
(o più sinteticamente, in inglese, ``prior'')
mentre
è chiamata distribuzione iniziale, o a priori
(o più sinteticamente, in inglese, ``prior'')
mentre
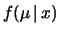 è la distribuzione finale, o
a posteriori, ove il ``prima'' e il ``dopo'' è rispetto
alla nuova osservazione
è la distribuzione finale, o
a posteriori, ove il ``prima'' e il ``dopo'' è rispetto
alla nuova osservazione  e non è da intendersi in modo strettamente
temporale. La funzione
e non è da intendersi in modo strettamente
temporale. La funzione
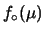 riassume lo stato di incertezza
su
riassume lo stato di incertezza
su 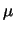 alla luce di tutte le conoscenze
a disposizione, a parte il verificarsi del dato sperimentale
alla luce di tutte le conoscenze
a disposizione, a parte il verificarsi del dato sperimentale  .
Quindi distribuzione iniziale e finale dovrebbero
essere scritte, più precisamente come:
.
Quindi distribuzione iniziale e finale dovrebbero
essere scritte, più precisamente come:




Next: Paura dei ``pregiudizi''? Inevitabilità
Up: Dalla probabilità degli effetti
Previous: Verosimiglianza
Indice
Giulio D'Agostini
2001-04-02