- ...scommessa1.1
- Si immagini di fare una scommessa
con puntate uguali contro una ipotetica persona che accetterebbe. Ci si rende
conto che se uno è fortemente propenso a scommettere in favore
del verificarsi di un evento, difficilmente si troverà una
persona che scommetta la stessa puntata contro,
a meno che non sia un ``pollo''.
Tale scommessa non è quindi equa. Variando invece il rapporto
delle puntate si può invece arrivare al punto in cui si è indecisi
se scommettere in favore o contro. Questi argomenti saranno trattati
quando si formalizzerà il concetto di probabilità. Per ora,
quando si parla di scommesse si pensi sempre di giocare alla pari
con l'intento di vincere.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... quinconce1.2
-
Con quinconce non si intende nient'altro che il modo di
disporre degli oggetti a righe sfalsate, come mostrato in figura
1.2.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Experiment''1.3
- Ad essere franchi
il quinconce meccanico
è una specie di assurdità didattica. Molto spesso infatti
la teoria del suo funzionamento viene presentata
come se fosse effettivamente la migliore descrizione del movimento delle
palline. Invece è lo strumento che viene costruito allo scopo
di rappresentare un modello di moto casuale che sia ha già in mente
e che nessun quinconce reale riuscirà mai a riprodurre.
Per questo è preferibile la ``sua simulazione'' al computer (il
termine simulazione è improprio in quanto
- ripetiamo - con il computer
non si prova a simulare
nessuna realtà, ma si ottiene semplicemente una
migliore realizzazione pratica
del modello di cammino casuale ideale).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
nell'estremo2.1
- La massa equivalente ai fini
dell'inerzia del sistema
e localizzata all'estremità della molla è pari a
un terzo della massa della molla.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ottiene2.2
-
Si noti come il valore di
 è riportato con 3 cifre
in quanto ulteriori cifre sarebbero ininfluenti alla fine del
risultato finale, come sarà chiarito nel paragrafo
3.4.
è riportato con 3 cifre
in quanto ulteriori cifre sarebbero ininfluenti alla fine del
risultato finale, come sarà chiarito nel paragrafo
3.4.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (ovvero3.1
-
Per ora consideriamo che l'incertezza della misura
sia dell'ordine di grandezza dell'ultima
cifra registrata.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...sostanzialmente3.2
- In questo caso in effetti due cifre
significative sembrano poche, ma tre sembrano troppe. È chiaro
che il numero di cifre significative
dipende dal sistema di numerazione adottato. Per esempio
le tre cifre significatice di ``125'' diventano
sette nel sistema binario (``1111101'') e si riducono a due
nel sistema esadecimale (``7D''). Vedremo al momento
opportuno come presentare il risultato con il numero di cifre
significative che dipende dalla qualità della misura
effettuata e non dall'uso del sistema decimale.
Un esempio estremo che mostra molto bene le grandi discontinuità prodotte
da un uso ferreo delle regole sulle cifre è il seguente:
Nel primo caso la cifra meno significativa è un decimo del
valore della grandezza, nel secondo un centesimo. Chi legge
soltanto i due risultati è indotto a pensare,
erroneamente, che i due risultati
derivino da esperimenti di diverso livello di qualità.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
addendi.3.3
- Per la serie ``ci vuole più a
dirlo che a farlo''...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
rispettivamente3.4
- L'uso del logaritmo decimale mostra
meglio l'effetto delle cifre significative del logaritmo
semplicemente dovute alla posizione della virgola. In questo caso si
otterrebbe rispettivamente 0.930, 4.930, -0.070 e -4.070.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
eccesso;3.5
- Le operazioni automatiche tendono a tranquillizzare
gli indecisi (per la serie ``lo ha detto il computer'').
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
analisi4.1
- Gli istogrammi del tipo di quelli mostrati in
figura 4.2 vanno visti come funzionali alla
costruzione delle tabelle
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... conteggi4.2
- Ricordiamo
che formando
segnali logici (``sì'' o ``no'')
dagli impulsi elettrici in uscita dal
fotomoltiplicatore si era già persa
l'informazione esatta sulla ionizzazione prodotta.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...ragionevole.4.3
- Qualcuno sarebbe tentato di parlare
di ipotesi corretta (``vera''). Non ci vuole molto a convincersi
che quando ha a che vedere con fenomeni aleatori, è raro che
si possa arrivare a definire certa, o vera, una data ipotesi.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... classe4.4
- Sottolineamo
che questi istogrammi sono utili non
soltanto per avere una rappresentazione grafica delle informazioni, ma
anche per contare le occorrenze di ciascuna classe.
Quindi, anche se per
ragioni didattiche le tabelle
4.1 e 4.2
sono state introdotte prima degli istogrammi di figura 4.2,
in realtà questi ultimi sono stati fatti per primi.
Per convincersi che tali istogrammi rappresentano
il modo più rapido e sicuro per contare occorrenze multiple
si suggerisce di provare, come esercizio,
a ricostruire le frequenze di conteggio
per
 s a partire dai dati di tabella 1.1.
s a partire dai dati di tabella 1.1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
isolati4.5
- Si noti come la pratica di considerare fuori norma
dei punti isolati può creare delle strane idee sugli eventi aleatori.
Ad esempio, gli eventi della figura 4.5 non hanno
assolutamente niente di ``anomalo'' rispetto a quelli che sono
nel mezzo della distribuzione.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
salienti.5.1
- Per una interessante analisi sulla nascita
della statistica, si veda I. Hacking, ``Il caso domato'', 1990
(il Saggiatore, 1994). Per esempio, a pag. 25
vi si legge la seguente il seguente passo scritto nel 1798
da J. Sinclair: ``Per statistica si intende in Germania
una ricerca fatta ai fini di accertare la forza politica di
un paese, o i problemi relativi agli affari si stato.''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... elementari5.2
- ``Elementare'' sta per una classe all'interno della
quale è impossibile - o irrilevante - differenziare
l'unità statistica rispetto
al carattere preso in esame.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... medio5.3
- Molto istruttiva
e divertente, a tale proposito, è la poesia di Trilussa in cui
il poeta ironizza sul fatto che
se uno mangia due polli e l'altro niente, ``secondo la statistica''
essi mangiano un pollo a testa.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... statistiche5.4
- Un derivato del campo di variabilità
è la semidispersione massima, definita come metà del campo
di variabilità.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
osservata5.5
- È chiaro che la scelta della grandezza opportuna
non è semplicemente parte della statistica descrittiva, ma in qualche modo
è legato alla statistica inferenziale, cioè al
problema di astrarre informazioni
di carattere generale con cui fare eventuali predizioni per le osservazioni
future a partire dai dati osservati. Questo argomento sarà trattato
al momento opportuno. Nel paragrafo 5.13 è discusso un
noto caso di interferenza fra statistica descrittiva e
statistica inferenziale
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
standard5.6
- La deviazione standard come è qui definita
è spesso indicata con
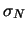 o
o 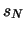 o
nelle calcolatrici tascabili. In molti testi il
simbolo
o
nelle calcolatrici tascabili. In molti testi il
simbolo 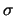 sarà riservato alla varianza
delle distribuzioni di probabilità e
sarà riservato alla varianza
delle distribuzioni di probabilità e 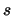 al suo stimatore,
definito tipicamente come
al suo stimatore,
definito tipicamente come
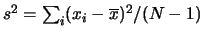 .
Come sarà commentato nel seguito (vedi paragrafi i bisogna
fare attenzione a non confondere problemi di statistica descrittiva
e problemi di statistica inferenziale. Inoltre bisogna anche abituarsi
ad una certa flessibilità. Per questo motivo indicheremo con
.
Come sarà commentato nel seguito (vedi paragrafi i bisogna
fare attenzione a non confondere problemi di statistica descrittiva
e problemi di statistica inferenziale. Inoltre bisogna anche abituarsi
ad una certa flessibilità. Per questo motivo indicheremo con
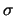 le deviazioni standard di distribuzioni
sia statistiche che di probabilità, a meno che non
sorgano ambiguità. Lo stesso discorso vale per il seimbolo `Var'.
le deviazioni standard di distribuzioni
sia statistiche che di probabilità, a meno che non
sorgano ambiguità. Lo stesso discorso vale per il seimbolo `Var'.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
misure.5.7
- Vedremo come il caso del contatore sia particolarmente
istruttivo in quanto mostra che in certi casi non è necessaria
alcuna
valutazione di dispersione - preliminare o dai dati spessi -
per la stima
dell'incertezza. Una sola misura, accompagnata da un modello
probabilistico del sistema, è sufficiente a fornire informazioni esaurienti
ai fini del risultato.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... male5.8
- Ad esempio,
la versione italiana di EXCEL della Microsoft traduce skewness
con ``asimmetria'', ma a quanto mi risulta gli statistici
italiani preferiscono decisamente skewness.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... media.5.9
- In generale,
il momento
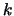 -mo rispetto a
-mo rispetto a 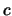 è definito come
è definito come
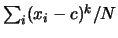 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... media5.10
- Nel
calcolo della deviazione standard
i dati sulle code devono compensare con l'``ampio braccio di leva
rispetto al baricentro'' l'alta frequenza di dati intorno al centro della
distribuzione.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...noto6.1
- In molti casi invece l'incertezza
è ricavata dalle fluttuazioni dei punti
sperimentali intorno all'andamento medio della curva
che li descrive. Allora le barre possono essere apportate
soltanto in una seconda fase di elaborazione dei dati sperimentali.
Questa nota serve a sottolineare che non c'è un imperativo categorico
di riportare i punti sperimentali sempre accompagnati dalle
barre di incertezza.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... distribuzione'',7.1
- Dire ``segue''
dà troppo l'idea che il numero aleatorio debba obbedire
ad una legge,
con tutti i fraintendimenti a cui tale punto di vista
conduce (``un numero ritardatario al lotto deve uscire più
facilmente di un altro per obbedire alle leggi della
probabilità''...).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ha7.2
- Si noti come il numero di
cifre con cui è espresso
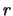 non segue
la regoletta che abbiamo introdotto precedentemente.
Come vedremo al momento di affrontare l'inferenza statistica,
l'incertezza su
non segue
la regoletta che abbiamo introdotto precedentemente.
Come vedremo al momento di affrontare l'inferenza statistica,
l'incertezza su 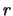 è pari a 0.0024. Quindi, essendo già
incerti sulla terza cifra decimale, arrotondiamo il
risultato a tale cifra.
è pari a 0.0024. Quindi, essendo già
incerti sulla terza cifra decimale, arrotondiamo il
risultato a tale cifra.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... multinomiale7.3
- Si noti
gli infiniti termini
corrispondenti a
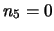 ,
, 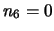 , etc., valgono tutti 1,
in quanto o
, etc., valgono tutti 1,
in quanto o 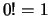 o
o 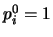 , e quindi possono essere ignorati.
, e quindi possono essere ignorati.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... dell'Oca.7.4
- Come è noto, questi giochi di società
si presentano con delle varianti. La simulazione che segue è stata
effettuata seguendo le regole della confezione Familienspiele
della Ravensburger: alle caselle 5, 9, 23, 41 e 45
si indietreggia di quanto si era avanzato; alle caselle 14, 18,
27, 32, 36 e 50 si avanza di quanto si era già avanzato;
(se dalla 18 si finisce poi alla 23, o dalla 50 alla 54, si
sta fermi un giro nella casella di arrivo); dalla casella 6 si avanza
alla 12 e dalla 42 si retrocede alla 30; alle caselle 19
e 52 si sta fermi
due giri; alla casella 31 si ha diritto ad un ulteriore lancio
di dadi (due); se si va oltre la casella 63 si rimbalza dei punti
che eccedono quelli per arrivare alla 63; si vince se si arriva
esattamente alla casella 63. Applicando alla lettera il regolamento,
si incontrano delle condizioni di loop infinito: se, essendo nella 23,
si ottiene 9 ai dati, o se dalla 31 si ottiene 5. Si è pertanto
deciso di arrestarsi dopo la prima retrocessione.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...misurabile)8.1
- Eventuali
aggettivi o precisazioni fra parentesi
nelle definizioni
possono essere omessi se non generano confusione.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... vero8.2
-
Secondo le più recenti raccomandazioni ISO,
anche l'aggettivo ``vero'' sarebbe superfluo. Per questioni didattiche
faremo uso il più delle volte dell'espressione ``valore vero'',
come contrapposta a ``valore misurato''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... laboratorio8.3
- In
realtà oggigiorno è molto più comodo
usare dispositivi a stato
solido, ad esempio un diodo Zener.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...misura8.4
- In inglese questa serie di operazioni è chiamata
``measurement'', e differisce da ``measure''.
C'è chi vorrebbe distiguere i concetti anche in italiano
e utilizzare il sostantivo ``misurazione per ``measurement''.
In realtà, per essere poi coerenti si dovrebbe anche dire
che la metrologia è la ``scienza della misurazione'',
parlare di metodo e di principio ``di misurazione''.
Nel mondo scientifico si usa comunemente misura
per esprimere entrambi i concetti
(nessuno parla di ``misurazione della massa del quark top'')
e questa sarà la convenzione
adottata in questo testo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... misura8.5
-
Questa distinzione differisce dalla definizione
secondo
la quale la misura diretta è quella derivante da ``un'operazione
di confronto tra la grandezza da misurare e un'altra grandezza
ad essa omogenea assunta come unità di misura''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... il 8.6
- La definizione ISO usa
l'articolo indeterminativo ``un'', consistentemente con la
definizione di valere vero.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...indeterminazione8.7
- In inglese
è ``uncertainty''. Per confronto può essere
utile sapere che il Principio di Indeterminazione
viene chiamato ``Uncertainty Principle''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... misurando'' 8.8
- Definizione ISO
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
vero8.9
- Si capisce quindi come la definizione
di valore vero come
``quello che si otterrebbe
dopo una serie infinita di misure con strumentazione
ideale'' non è migliore di quella ISO, anzi, questa dà
l'illusione che questo valore sia, almeno idealmente, unico,
mentre la definizione ISO tiene conto che le misure vengono
eseguite in condizioni reali e con tutte le cause
di incertezza che saranno elencate in questo paragrafo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...accuratezza8.10
-
I termini inglesi equivalenti sono precision e accuracy.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...ripetitibilità8.11
- Per le definizioni
di ripetitibilità e riproducibilità
vedi i paragrafi 10.2 e 11.2.1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... misura8.12
-
È da notare che a volte si incontra
il termine "calibrazione" utilizzato per indicare
l'operazione di aggiustamento.
Per taratura si intende invece l'operazione mediante la quale,
applicando allo strumento sollecitazioni note, si determina la
corrispondenza fra i valori dell'uscita e la grandezza da misurare.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... misura8.13
-
Nel testo inglese delle norme DIN compare come material measure.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
l'aggiornamento9.1
- Ma anche in questo caso si è imparato
qualcosa, cioè che il termometro non funziona...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
critica9.2
- Molto spesso si pensa che l'unico metodo scientifico
valido sia quello della falsificazione.
Non ci sono dubbi che, se una teoria
non è in grado di descrivere i risultati di
un esperimento,
essa vada scartata o modificata. Ma poiché non è possibile
dimostrare la certezza di una teoria, diventa impossibile decidere
fra tutte le (infinite) ipotesi non falsificate.
Il metodo probabilistico
permette di fornire una scala di credibilità a tutte
le ipotesi considerate (o rapporti di credibilità fra ogni
coppia di ipotesi).
Un caso in cui il metodo
di falsificazione è completamente inadeguato
è quello relativo agli incertezze di misura.
Infatti, prendendo alla lettera
tale metodo, si sarebbe autorizzati soltanto a
verificare se il valore osservato sullo strumento
è compatibile o no con un valore
vero, niente di più. Si capisce come, con queste
premesse, non si possa fare
molta strada.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... osservare9.3
- Attenzione a non confondere la probabilità
di osservare un certo valore
 , subordinatamente ad un certo valore
di
, subordinatamente ad un certo valore
di 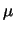 , con la probabilità del valore che è stato
effettivamente osservato. Essendo questo un numero certo
(a meno di non essere ubriachi), ad esso non si applica il
concetto di probabilità.
Così pure, si faccia attenzione a non chiamare
, con la probabilità del valore che è stato
effettivamente osservato. Essendo questo un numero certo
(a meno di non essere ubriachi), ad esso non si applica il
concetto di probabilità.
Così pure, si faccia attenzione a non chiamare
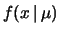 ``probabilità che
``probabilità che  venga da
venga da 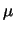 '' (il nome corretto - trascurando
il fatto inessenziale che si tratta di una densità di probabilità e non
di una probabilità - è ``probabilità di
'' (il nome corretto - trascurando
il fatto inessenziale che si tratta di una densità di probabilità e non
di una probabilità - è ``probabilità di  ,
dato un certo valore
,
dato un certo valore 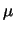 '',
che è chiaramente ben altra cosa!).
'',
che è chiaramente ben altra cosa!).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
dell'osservazione9.4
- Si noti l'uso dello stesso simbolo
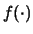 per indicare funzioni di diverse variabili, anche se
sarebbe formalmente più corretta una scrittura della
(9.4) del tipo:
con
per indicare funzioni di diverse variabili, anche se
sarebbe formalmente più corretta una scrittura della
(9.4) del tipo:
con
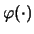 ,
,
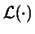 e
e
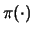 che ricordano dal nome, rispettivamente, la finale,
la verosimiglianza (in inglese likelihood) e la
prior.
che ricordano dal nome, rispettivamente, la finale,
la verosimiglianza (in inglese likelihood) e la
prior.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Poincar\'e9.5
- H. Poincaré, ``Scienza e Ipotesi'',
molto interessante il capitolo XI sul calcolo
delle probabilità.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
dell'esperimento.9.6
- Si potrebbe obiettare: ma non è sufficiente
riportare semplicemente i dati osservati? Se da questi il calcolo
delle verosimiglianze è banale, allora non c'è nessun problema.
Ma negli esperimenti complicati la dipendenza dei dati osservabili
dall'ipotesi fisica può essere talmente complessa che solamente
chi ha fatto l'esperimento è in grado di calcolare le verosimiglianze.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... misura10.1
- Le prior non devono mai sparire
completamente dalla mente, ma devono servire a vigilare
attentamente il flusso dei dati e intervenire
al minimo sospetto che qualcosa non vada!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Bayes10.2
- Una prior uniforme e una verosimiglianza gaussiana
producono, in virtù della (9.5),
il seguente risultato:
in cui nell'ultimo passaggio sono stati invertiti
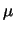 e
e  , al fine di ricordare che la variabile
della nuova funzione è
, al fine di ricordare che la variabile
della nuova funzione è 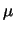 e non più
e non più  (questo
diventa il parametro che dà il centro della distribuzione).
Ne segue che il valore vero è distribuito intorno
al valore osservato secondo una gaussiana avente la stessa
deviazione standard della verosimiglianza:
(questo
diventa il parametro che dà il centro della distribuzione).
Ne segue che il valore vero è distribuito intorno
al valore osservato secondo una gaussiana avente la stessa
deviazione standard della verosimiglianza:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... tipo10.3
- Il fatto che il solo valore
della media aritmetica sia in grado di produrre una inferenza
statistica della stessa qualità dei singoli valori osservati
è legato al concetto statistico di ``sufficienza''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... media10.4
- Si ricorda che,
ai fini del calcolo pratico, essa è valutata come:
ove
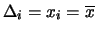 sta ad indicare, secondo la convenzione delle
calcolatrici tascabili,
che la varianza è calcolata come media dei quadrati
degli scarti.
sta ad indicare, secondo la convenzione delle
calcolatrici tascabili,
che la varianza è calcolata come media dei quadrati
degli scarti.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... trascurabili10.5
- In realtà questo è una
condizione non necessaria, legata ad un modo semplicistico di vedere
le cose: anche se ci sono incertezze sulle ascisse, queste possono
essere riflesse su quelle delle ordinate e la soluzione pratica non cambia.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... successive10.6
- Un caso tipico è quello
di risultati correlati. In alcuni casi anche la terza o la quarta
cifra dell'incertezza può diventare cruciale.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fisiche10.7
-
Particle Data Group, Phys. Rev. D50 (1994) 1173.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
finora.10.8
- Per chiarire il concetto,
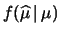 può
essere stato ottenuto come media aritmetica, come ad esempio
mostrato nella (10.2), ovvero
può
essere stato ottenuto come media aritmetica, come ad esempio
mostrato nella (10.2), ovvero
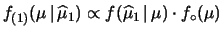 . I valori veramente osservati
sono gli
. I valori veramente osservati
sono gli 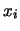 , mentre
, mentre
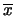 è ottenuto da un'operazione
matematica eseguita su di essi. Comunque, si può dimostrare
che la conoscenza della sola media fornisce lo stesso grado
di conoscenza su
è ottenuto da un'operazione
matematica eseguita su di essi. Comunque, si può dimostrare
che la conoscenza della sola media fornisce lo stesso grado
di conoscenza su 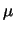 di quello ottenibile dall'insieme dei valori
osservati. Questa equivalenza è legata al
concetto della cosiddetta sufficienza statistica.
di quello ottenibile dall'insieme dei valori
osservati. Questa equivalenza è legata al
concetto della cosiddetta sufficienza statistica.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... risultato10.9
- Come si vede facilmente,
si ottiene un risultato del tutto equivalente
a quello cui si sarebbe arrivati
partendo dal
punto 2 del paragrafo 10.4.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... indirette11.1
- Vedremo come entrano in gioco anche
più per
valutare effetti di errori sistematici di misure dirette.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
riproducibilità.11.2
- La Guida ISO
definisce reproducibility (of results of measurements)
``closeness of the agreement between the results of measurements of
the same measurand carried out under changed conditions of measurement''
(i risultati si intendono già corretti per
eventuali errori sistematici noti).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
gaussiana11.3
- In realtà non c'è bisogno che la distribuzione
sia normale, in quanto faremo uso soltanto delle proprietà generali
della varianza. Anche dal punto di vista pratico, è più frequente
il caso di una distribuzione uniforme o triangolare.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
accorgimento11.4
- Ad esempio un voltmetro può
essere calibrato in modo relativo (rispetto al valore di fondo scala)
utilizzando un partitore di precisione: ogni deviazione dalla
linearità sarà imputato al comportamento del voltmetro e
la lettura potrà essere corretta. Per fare un buon
partitore economico è sufficiente prendere una ventina di
resistori all'1% tutti uguali e presi nuovi dalla stessa
striscia con cui sono confezionati.
Le variazioni relative di resistenza
sono ben inferiori all'1% e la loro combinazione riduce ancora di più
le incertezze relative.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... correlazione11.5
- Questo approccio
molto euristico potrebbe servire anche a chi lo conosce
da testi di probabilità.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(lineare11.6
- Questo è un punto importante, ma sul
quale purtroppo non possiamo entrare in dettaglio.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... quantity11.7
- Per
``grandezza d'ingresso'' la Guida ISO intende tutte
le grandezze che contribuiscono alla valutazione del valore
della grandezza di interesse (costanti di calibrazione, parametri di
influenza, valori tabulati, risultati di esperimenti precedenti, etc.).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... riferimento''11.8
- I valori che
seguono, la formula (11.35) e la tabella 11.2
sono presi da
F. Kohlrausch,
``Praktische Physik'', B.G. Teubner Stuttgart 1986. La
sezione 72 sulla densità dell'aria è curata da M. Kochsieck
dell'istituto tedesco di metrologia di Braunschweig.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ottengono11.9
- E.R. Cohen and B.N. Taylor,
Rev. Mod. Phys. 59 (1987) 1121.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... misurano11.10
-
Misura realmente effettuata in data 2/5/93. I 420
resistori da cui è stato estratto il campione sono stati
successivamente utilizzati per le esercitazioni di
laboratorio.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
volumi11.11
- Questo problema è tratto dal lavoro di R.B. Lam e T.L.
Isenhour, ``Minimizing relative error in the preparation of
standard solutions by judicious choice of volumetric glassware'',
pubblicato su Anal. Chem 52 (1980) 1158,
in cui gli autori hanno studiato i 250000 modi di effettuare diluizioni
a 1, 2 o 3 passi utilizzando strumentazione commerciale standard.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
riduce12.1
- Se si prova a fare i conti
con le regole delle matematica elementare si trovano risultati
divergenti. In realtà il limite va fatto integrando la
funzione per tutti i valori di
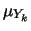 e quindi fare il limite per
e quindi fare il limite per
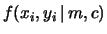 . Chi è familiare con elementi di matematica
avanzata riconosce in tale operazione l'uso della
. Chi è familiare con elementi di matematica
avanzata riconosce in tale operazione l'uso della  di Dirac
(vedi anche prossimo paragrafo).
di Dirac
(vedi anche prossimo paragrafo).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... infatti12.2
- Si noti che questa espressione è valida
per variabili continue. Per variabili discrete equispaziate
fra
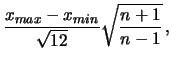 e
e  , la formula esatta
è
che tende alla deviazione standard del caso continuo quando
, la formula esatta
è
che tende alla deviazione standard del caso continuo quando
 è molto grande. Comunque, già per
è molto grande. Comunque, già per 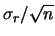 il fattore
correttivo è del 20% e per
il fattore
correttivo è del 20% e per  è del 10%.
è del 10%.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
all'incertezza12.3
- Ovviamente la valutazione di effetti
sistematici rimane invariata
se i parametri della retta sono valutati con i minimi
quadrati anziché con l'analisi grafica.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 12.4
- Per
quanto riguarda il numero di cifre significative,
si noti come ne sia stata aggiunta una in più rispetto
alle regolette usuali. Esse verranno aggiustate in seguito
alla luce di
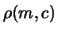 e di
e di 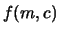 . Nel caso in
cui l'esperienza non preveda un'analisi completa delle incertezze
di misura sarebbe stato sufficiente scrivere
. Nel caso in
cui l'esperienza non preveda un'analisi completa delle incertezze
di misura sarebbe stato sufficiente scrivere
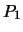 m kg
m kg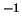 e
e 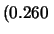 cm.
cm.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
soddisfacente12.5
- Le piccole differenze
numeriche sono dovute
all'uso della formula approssimata per il braccio di leva.
Corretto per il fattore
(legato alla deviazione standard di una distribuzione uniforme discreta),
esso diventa 0.180kg, da cui ne segue un risultato
praticamente identico a quello ottenuto mediante programma:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 1.000 kg12.6
- Si noti come nella propagazione
non si debba tener conto di un'eventuale incertezza sulla massa
se essa è simile a quella dei pesetti con i quali sono
state effettuate le misure, in quanto questo contributo è già compreso
in
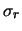 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... baricentro.12.7
- Come abbiamo già fatto notare,
il sistema del baricentro è molto conveniente, in quanto
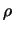 si annulla. L'espressione di
si annulla. L'espressione di 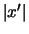 è particolarmente
semplice e istruttiva:
Si riconosce la combinazione in quadratura dell'incertezza
dovuta all'intercetta con quella del coefficiente angolare
``proiettata'' ad una distanza
è particolarmente
semplice e istruttiva:
Si riconosce la combinazione in quadratura dell'incertezza
dovuta all'intercetta con quella del coefficiente angolare
``proiettata'' ad una distanza
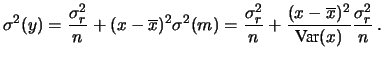 dal baricentro.
dal baricentro.
Siccome 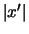 deve essere invariante per traslazioni,
antitrasformando da
deve essere invariante per traslazioni,
antitrasformando da 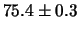 a
a  , otteniamo la formula
, otteniamo la formula
Si vede quindi come la previsione sull'ordinata abbia
una precisione che è massima in corrispondenza del baricentro
dei punti e si deteriora quando ci si allontana dalla regione
in cui sono state effettuate le misure.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
differenze12.8
- Naturalmente, per
ottenere la massima accuratezza sulla precisione dei parametri
sarebbe stato meglio misurare individualmente ciascuno
dei pesetti, al fine di ridurre
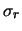 , ma a questo livello
non ne vale la pena.
, ma a questo livello
non ne vale la pena.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nell'inter\-vallo12.9
- I due estremi sono 57 e 243 se
si usa il valore di
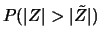 . La differenza
fra i risultati, che va confrontata con l'ampiezza dell'intervallo, è
assolutamente trascurabile.
. La differenza
fra i risultati, che va confrontata con l'ampiezza dell'intervallo, è
assolutamente trascurabile.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... mancante12.10
- Il test di ipotesi di compatibilità
fra i due risultati effettuato mediante il
controllo se lo zero è compreso nell'intervallo
di fiducia di
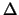 è indipendente dal segno di
è indipendente dal segno di 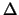 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... teorica12.11
-
Da notare come nella (12.24) delle dispense al denominatore ci
sia per ogni
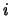 una sua
una sua 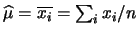 . Esso rappresenta
il caso più generale in cui ciascuna delle
. Esso rappresenta
il caso più generale in cui ciascuna delle 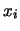 fluttua dal valore
vero con una propria
fluttua dal valore
vero con una propria 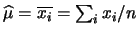 di cui la deviazione standard
empirica è la migliore stima. Nelle misure di conteggio, con ipotesi
che il valore medio sia comune, la migliore stima di
di cui la deviazione standard
empirica è la migliore stima. Nelle misure di conteggio, con ipotesi
che il valore medio sia comune, la migliore stima di 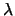 determina anche la migliore stima di
determina anche la migliore stima di 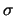 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... relative12.12
-
rispetto alla soluzione precedente
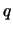 corrisponde al parametro
corrisponde al parametro
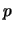 della binomiale e
della binomiale e 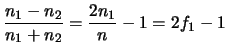 a
a 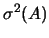
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... risultati12.13
-
Per l'esattezza, il
valore di
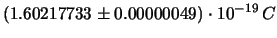 riportato da Cohen e Taylor è leggermente
diverso:
137.0359895(61). Ci sono evidentemente piccoli problemi di
arrotondamento. Se si esegue il conto con un calcolatorino
scientifico a 10 cifre il risultato è 137.0359908 (61)!
riportato da Cohen e Taylor è leggermente
diverso:
137.0359895(61). Ci sono evidentemente piccoli problemi di
arrotondamento. Se si esegue il conto con un calcolatorino
scientifico a 10 cifre il risultato è 137.0359908 (61)!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... uniforme12.14
- Ricordiamo che in mancanza di accertamenti
questa è la distribuzione da utilizzare [ vedi nota a pag. 136 ].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... simulazioneA.1
- Non ci sarebbe alcun bisogno
di simulare il processo al computer, dato che la soluzione
può essere ottenuta analiticamente mediante il
calcolo delle probabilità, ma l'esperienza mi insegna
che le simulazioni possono essere più convincenti per alcune persone.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
altriA.2
- Ci si potrebbe chiedere: come mai questo processo
non porta ad un collasso? Semplicemente perché nei laboratori
non si seguono queste regole e, invece di nascondere la testa
nella sabbia degli errori massimi, si cerca di ricalibrare
in continuazione strumenti e procedure. Questo è
quanto dovrebbe imparare subito
anche lo studente
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
puerileA.3
- Questo aspetto psicologico non
riguarda soltanto gli studenti. Non è raro vedere anche
nella ricerca avanzata risultati in sorprendente accordo
fra di loro o con predizioni teoriche nonostante le loro
enormi barre di incertezza, o fisici sperimentali preoccupati
se i loro valori differiscono di un paio di
deviazioni standard da una ``solida predizione'' o da un
risultato precedente.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... letturaA.4
- A volte lo si sente chiamare
anche errore di sensibilità, o addirittura semplicemente
``sensibilità'' (in una nota per studenti si legge testualmente:
``l'indeterminazione su tali grandezze può essere presa pari alla
sensibilità del termometro impiegato, ovvero mezza tacca'').
In questo caso ``sensibilità'' starebbe per ``risoluzione''
(vedi capitolo 8). È raccomandabile
utilizzare il termine ``sensibilità'' per indicare ...
la sensibilità, ovvero,
detto alla buona, ``il rapporto fra la variazione della risposta
e la variazione dello stimolo''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... divisioni.''
A.5
- Essere praticamente sicuri che
il valore sia entro il 1/5 di divisione, vuol dire
che, se ci si sforza al interpolare al meglio, ci
si aspetta una deviazione standard dell'errore di
lettura di circa
 divisioni,
compatibile al valore di
divisioni,
compatibile al valore di
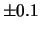 che si osserva
sperimentalmente.
che si osserva
sperimentalmente.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
taccheA.6
- Perché non cambiare strumento?
Domanda legittimissima. Il problema è che questo non è sempre possibile.
Quindi è importante, all'occorrenza, imparare a sfruttare tutta
la potenzialità degli strumenti a disposizione. Queste dovrebbero
essere le regole del gioco
sulle quale sviluppare un corso di teoria
e pratica di valutazione delle incertezze di misure.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... secondoA.7
- Si noti inoltre che, quando si misura
una grandezza fisica (
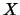 ) in funzione del tempo (
) in funzione del tempo (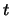 ), non ha molto
senso parlare di errori su
), non ha molto
senso parlare di errori su 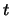 e su
e su 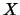 ,
in quanto ogni differenza dell'istante di lettura dal
tempo nominale si rifletterà in un errore sulla
grandezza fisica. Quindi, ai fini del risultato finale,
è più che ragionevole attribuire tutto l'errore a
,
in quanto ogni differenza dell'istante di lettura dal
tempo nominale si rifletterà in un errore sulla
grandezza fisica. Quindi, ai fini del risultato finale,
è più che ragionevole attribuire tutto l'errore a 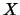 e considerare
e considerare 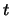 esente da errore (si veda anche
il paragrafo 10.5.2).
esente da errore (si veda anche
il paragrafo 10.5.2).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... QuinnA.8
- T.J. Quinn, ``The
beam balance as an instrument for very
precise weighing'', Meas. Sci. Technol., 3(1992), 141.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![$\displaystyle f(x\,\vert\,\mu) \propto
\exp{\left[-\frac{(x-\mu)^2}{2\,\sigma^2_r}\right]}$](img1309.png)
![$\displaystyle \exp{\left[-\frac{(\mu-x)^2}{2\,\sigma^2_r}\right]}\,,$](img1310.png)
e quindi fare il limite per
. Chi è familiare con elementi di matematica avanzata riconosce in tale operazione l'uso della
di Dirac (vedi anche prossimo paragrafo).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .e
, la formula esatta è
che tende alla deviazione standard del caso continuo quando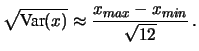
è molto grande. Comunque, già per
il fattore correttivo è del 20% e per
è del 10%.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .e di
. Nel caso in cui l'esperienza non preveda un'analisi completa delle incertezze di misura sarebbe stato sufficiente scrivere
m kg
e
cm.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .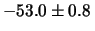
mm
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .si annulla. L'espressione di
è particolarmente semplice e istruttiva:
Si riconosce la combinazione in quadratura dell'incertezza dovuta all'intercetta con quella del coefficiente angolare ``proiettata'' ad una distanza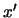
dal baricentro.
deve essere invariante per traslazioni, antitrasformando da
a
, otteniamo la formula
Si vede quindi come la previsione sull'ordinata abbia una precisione che è massima in corrispondenza del baricentro dei punti e si deteriora quando ci si allontana dalla regione in cui sono state effettuate le misure.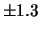 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . ., ma a questo livello non ne vale la pena.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. La differenza fra i risultati, che va confrontata con l'ampiezza dell'intervallo, è assolutamente trascurabile.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .è indipendente dal segno di
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .una sua
. Esso rappresenta il caso più generale in cui ciascuna delle
fluttua dal valore vero con una propria
di cui la deviazione standard empirica è la migliore stima. Nelle misure di conteggio, con ipotesi che il valore medio sia comune, la migliore stima di
determina anche la migliore stima di
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .corrisponde al parametro
della binomiale e
a
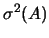 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .riportato da Cohen e Taylor è leggermente diverso: 137.0359895(61). Ci sono evidentemente piccoli problemi di arrotondamento. Se si esegue il conto con un calcolatorino scientifico a 10 cifre il risultato è 137.0359908 (61)!
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .divisioni, compatibile al valore di
che si osserva sperimentalmente.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .) in funzione del tempo (
), non ha molto senso parlare di errori su
e su
, in quanto ogni differenza dell'istante di lettura dal tempo nominale si rifletterà in un errore sulla grandezza fisica. Quindi, ai fini del risultato finale, è più che ragionevole attribuire tutto l'errore a
e considerare
esente da errore (si veda anche il paragrafo 10.5.2).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .