



Next: Misure di posizione
Up: Descrizione quantitativa dei dati
Previous: Statistica descrittiva e statistica
Indice
Introduciamo innanzitutto il concetto di
distribuzione statistica.
Le tabelle 4.1 e 4.2 e le figure
4.1 e 4.2 mostrano come
sono distribuiti dei dati sperimentali di interesse,
rispettivamente
l'età dei cittadini
tedeschi e i conteggi registrati in un certo intervallo di tempo.
Abbiamo detto prima come le tabelle e gli istogrammi si ottengono
dal conteggio delle occorrenze di ciascuna delle classi in cui
sono stati raggruppate le informazioni.
Nei due casi illustrati per ogni unità statistica (il singolo
cittadino tedesco o la singola misura) si era interessati
ad un solo carattere (età e numero di
conteggi, rispettivamente). In genere la scelta del carattere
a cui ci si interessa può
essere arbitraria e dipende dall'applicazione particolare.
Ad esempio, trattandosi di studenti universitari si può essere
interessati al tipo di maturità conseguita, alla città di
provenienza, al sesso o al colore dei capelli. A volte i caratteri
possono essere delle informazioni quantitative, come il voto
riportato alla maturità, il numero di esami sostenuti, l'altezza
o il peso. Questo dato statistico (quantitativo)
può essere discreto (come voto ed esami sostenuti)
o - almeno in principio - continuo (come altezza e peso).
Altra ovvia considerazione è che, per ciascun carattere preso
in considerazione, ogni unità statistica (l'individuo o il
singolo risultato di una misura) appartenente
ad una popolazione (la totalità
degli individui o dei dati sperimentali) appartenga ad una ed
una sola classe (lo studente non può aver conseguito 42
e 60 alla maturità), mentre non è vero il
contrario (molti studenti possono avere avuto lo stesso voto).
Non sempre i dati sono relativi
all'intera popolazione:
a volte si hanno dati relativi soltanto ad un campione della
popolazione; altre popolazioni
possono essere virtualmente infinite
- come quella legata a tutte le
misure possibili di una certa grandezza fisica.
Si dice che
i dati statistici (quantitativi)
costituiscono una distribuzione statistica
quando a
ciascuno di essi è associato il numero di volte
con il quale si è verificato.
Introduciamo dei simboli per operare sulle distribuzioni statistiche.
Al fine di alleggerire le formule eviteremo d'ora innanzi di
scrivere esplicitamente gli estremi delle sommatorie, a meno
che non ci siano ambiguità oppure, saltuariamente, per rinfrescare
le convenzioni. Quindi saranno generalmente da intendersi le
seguenti abbreviazioni:
Nell'effettuare la classificazione dei dati sperimentali possono
capitare due situazioni.
- I valori numerici (
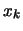 ) delle classi sono tutti i valori numerici
assunti dalle unità statistiche (
) delle classi sono tutti i valori numerici
assunti dalle unità statistiche (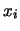 ),
come ad esempio le classificazioni
delle tabelle 4.1 e 4.2.
),
come ad esempio le classificazioni
delle tabelle 4.1 e 4.2.
- I valori numerici delle classi sono inferiori a quelli delle
unità statistiche. Questo succede se il numero di possibili classi
è talmente elevato che è preferibile raggruppare più classi
elementari5.2 contigue. Viene così persa l'informazione degli esatti valori
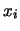 acquistati dai dati sperimentali originali e per valore numerico
della classe si prende semplicemente il punto medio di ciascuno
degli intervalli che definiscono la classe. Si ha sempre questo secondo caso
quando i valori numerici delle unità statistiche sono
continui.
acquistati dai dati sperimentali originali e per valore numerico
della classe si prende semplicemente il punto medio di ciascuno
degli intervalli che definiscono la classe. Si ha sempre questo secondo caso
quando i valori numerici delle unità statistiche sono
continui.
La seconda situazione avrà delle conseguenze
sul valore numerico dei riassunti statistici,
i quali differiranno
da quelli che si ottengono dai dati non raggruppati. Comunque
la differenza è in genere trascurabile, specialmente se si hanno
molte classi e la distribuzione
dei dati all'interno di esse
è abbastanza ``regolare'' (vedi esempio nel paragrafo
5.8).
Come esempio eseguiamo una suddivisione in classi dei tempi di attesa
per 1 conteggio (tabella 1.2).
La tabella 5.1 mostra due modi
per riunire in classi questi dati continui. Nel secondo raggruppamento
le classi
sono di diversa ampiezza. Sarà interessante vedere le variazioni
dei risultati dovuti ai raggruppamenti in classi.
Tabella:
Due modi di raggruppamento in classe dei valori dei
tempi di attesa per un conteggio (tabella 1.2).
|
Raggruppamento 1 |
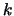 |
estremi |
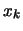 |
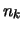 |
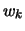 |
|
1 |
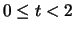 |
1 |
30 |
0.30 |
|
2 |
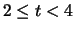 |
3 |
20 |
0.20 |
|
3 |
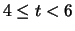 |
5 |
15 |
0.15 |
|
4 |
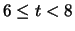 |
7 |
8 |
0.08 |
|
5 |
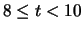 |
9 |
10 |
0.10 |
|
6 |
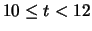 |
11 |
8 |
0.08 |
|
7 |
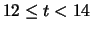 |
13 |
2 |
0.02 |
|
8 |
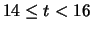 |
15 |
2 |
0.02 |
|
9 |
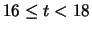 |
17 |
3 |
0.03 |
|
10 |
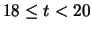 |
19 |
1 |
0.01 |
|
11 |
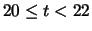 |
21 |
1 |
0.01 |
|
Raggruppamento 2 |
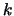 |
estremi |
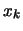 |
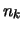 |
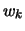 |
|
1 |
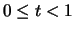 |
0.5 |
19 |
0.19 |
|
2 |
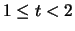 |
1.5 |
11 |
0.11 |
|
3 |
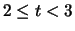 |
2.5 |
13 |
0.13 |
|
4 |
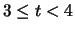 |
3.5 |
7 |
0.07 |
|
5 |
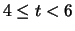 |
5 |
15 |
0.15 |
|
6 |
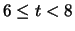 |
7 |
8 |
0.08 |
|
7 |
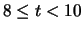 |
9 |
10 |
0.10 |
|
8 |
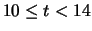 |
12 |
10 |
0.10 |
|
9 |
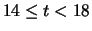 |
16 |
5 |
0.05 |
|
10 |
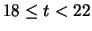 |
20 |
2 |
0.02 |
|




Next: Misure di posizione
Up: Descrizione quantitativa dei dati
Previous: Statistica descrittiva e statistica
Indice
Giulio D'Agostini
2001-04-02