



Next: pzd100Box plot
Up: Descrizione grafica dei dati
Previous: Riduzione dei dati
Indice
Tabelle, istogrammi e
diagrammi a barre
Tornando alla nostra misura di radioattività con il
contatore a scintillazione, un modo per
presentare le informazioni in forma più compatta
è quello di raccoglierle in
tabelle in cui le classi omogenee
sono rappresentate dai conteggi registrati
(tabelle 4.1 e 4.2).
Il numero di volte in cui si è verificato un certo conteggio
è chiamato frequenza.
L'informazione persa in questa riduzione dei dati
è quella della sequenza temporale
con cui si sono verificati i conteggi4.2.
Essa è comunque
inessenziale se si presuppone
che la radioattività praticamente non cambia
nel tempo o, meglio ancora,
se è controllato che tale ipotesi è
ragionevole.4.3
Figura:
Istogrammi dei risultati dell'esperienza
del contatore. Il simbolo ``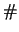 '' sta per ``numero''. Il termine ``evento''
è qui usato - come avviene usualmente - nel senso di ``occorrenza''
o ``numero di volte''.
'' sta per ``numero''. Il termine ``evento''
è qui usato - come avviene usualmente - nel senso di ``occorrenza''
o ``numero di volte''.
 |
Il modo più semplice
di rappresentare graficamente le frequenze di conteggio
consiste nel costruire un istogramma per ogni
serie di misure (figura 4.2).
L'uso di rappresentazioni grafiche di questo tipo è talmente
comune sia nei libri che nei mass media che la loro lettura
non necessita di alcuna spiegazione. Qualche parola va invece spesa
sul modo di realizzarli. Gli istogrammi mostrati in figura
4.2 sono fra quelli
che più frequentemente si incontrano in laboratorio,
specialmente per dare un'occhiata veloce ad una
manciata di dati
e per contare le occorrenze
di ciascuna classe4.4.
In genere per operazioni più complesse entrano immediatamente
in gioco i calcolatori. Osservando la figura si notano tre tipi
di istogrammi.
- In quello relativo alle misure da
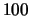 s c'è una crocetta
per ogni occorrenza di un certo numero di conteggi (il simbolo
``
s c'è una crocetta
per ogni occorrenza di un certo numero di conteggi (il simbolo
``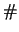 '' sta per ``numero di''). Le occorrenze sono usualmente
chiamate anche ``eventi'' dai fisici,
anche se vedremo che nello studio
della probabilità tale nome verrà utilizzato con altro
significato (è opportuno abituarsi subito a
qualche inevitabile ambiguità di linguaggio, ricordandosi che,
come scrisse Wittgenstein
``un significato di una parola
è un suo mode del suo impiego'').
'' sta per ``numero di''). Le occorrenze sono usualmente
chiamate anche ``eventi'' dai fisici,
anche se vedremo che nello studio
della probabilità tale nome verrà utilizzato con altro
significato (è opportuno abituarsi subito a
qualche inevitabile ambiguità di linguaggio, ricordandosi che,
come scrisse Wittgenstein
``un significato di una parola
è un suo mode del suo impiego'').
- Nei quattro istogrammi in alto il numero di eventi è talmente
elevato che la tecnica precedente non può funzionare. È preferibile
allora mettere delle barrettine verticali per ogni evento
e raggruppare gli eventi con un tratto obliquo
ogni cinque eventi.
- Nelle misure da
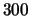 s si ha invece un problema di
dispersione di dati sull'asse delle ascisse. Anche se si fossero
tracciate delle crocette più piccole, la dispersione
sarebbe tale da far perdere
la visione d'insieme. Si è allora preferito
formare nuove classi raggruppando conteggi contigui.
Il numero tracciato sull'asse delle ascisse rappresenta il limite
inferiore della classe. Ovvero vengono riportati all'interno
di un bin gli eventi per i quali
è valida la relazione
s si ha invece un problema di
dispersione di dati sull'asse delle ascisse. Anche se si fossero
tracciate delle crocette più piccole, la dispersione
sarebbe tale da far perdere
la visione d'insieme. Si è allora preferito
formare nuove classi raggruppando conteggi contigui.
Il numero tracciato sull'asse delle ascisse rappresenta il limite
inferiore della classe. Ovvero vengono riportati all'interno
di un bin gli eventi per i quali
è valida la relazione
limite inferiore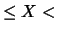 limite superiore limite superiore |
(4.1) |
L'istogramma indica, ad esempio,
che si sono verificati 10 eventi per i quali
il numero di conteggi è maggiore o uguale di 60 e minore di 62.
A differenza degli altri due tipi di istogrammi,
qui si è persa l'informazione della quantità di eventi per numero
di conteggi all'interno di ciascuna classe.
Quest'ultimo tipo di istogramma è quello comunemente
utilizzato se
un risultato si può presentare in un grande numero
di classi. Tale numero può diventare
virtualmente
infinito per grandezze i cui valori possono assumere
valori con continuità - dal punto di vista pratico, non dal
punto di vista puramente matematico - in un certo intervallo.
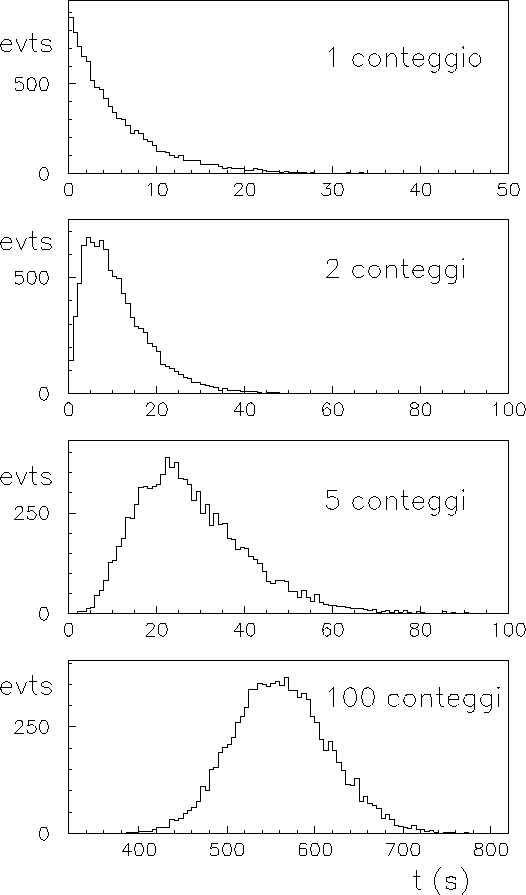
Un esempio di questa applicazione è mostrato in figura
4.3, dove sono istogrammati i tempi di
attesa per ottenere un numero prefissato di conteggi. Per meglio mostrare
le distribuzioni dei tempi questi
istogrammi sono ottenuti utilizzando 10 000 eventi ottenuti nelle
stesse condizioni di quelli della tabella 1.2.
000 eventi ottenuti nelle
stesse condizioni di quelli della tabella 1.2.
Figura:
Istogrammi dei tempi di attesa per 1, 2, 5 e 100 conteggi,
basati ciascuno su 10000 eventi simulati (i dati
simulati della tabella 1.2
ne rappresentano un piccolo sotto-campione).
``evts'' è un altro modo di scrivere ``numero di eventi''.
Un altro modo di rappresentare gli stessi eventi è mostrato
in figura 6.7.
 |
È da notare come i quattro istogrammi in alto,
della figura 4.2,
realizzati con le stesse scale in ascissa e ordinata,
si prestino più facilmente a confronti degli altri due.
Questo insegna che, quando è possibile,
è preferibile procedere in questo modo (ancor meglio
se gli istogrammi possono essere disposti in colonna).
A volte nemmeno l'informazione della frequenza di ciascuna classe
è importante. Ad esempio, il fatto che per 56 volte
si siano verificati zero conteggi nelle
misure da 3 secondi dipende dal numero totale di misure effettuate.
Se invece di 100 misure ne avessimo eseguite 1000 avremmo
ragionevolmente ottenuto
un numero di zeri circa 10 volte maggiore.
Ben diverso è invece il significato
del rapporto fra il numero con cui si verificano zero conteggi
e quello con cui se ne verifica uno. Ci attendiamo
infatti che tale rapporto resti circa costante
all'aumentare del numero
di misure. Invece del rapporto fra le frequenze di
due classi è preferibile allora calcolare la
frequenza relativa, ovvero la frequenza diviso il numero
di prove (le misure effettuate, nel nostro caso).
Spesso per comodità si preferisce evitare
l'uso persistente di numeri minori di uno e si passa
alle frequenze percentuali. Questa operazione è nota a tutti,
ma bisogna fare attenzione a scrivere esplicitamente il simbolo
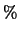 , e a leggere correttamente i valori graficati, per non
incorrere nel rischio di sbagliare di un fattore 100.
I 6 ``istogrammi'' di figura 4.4 mostrano
le frequenze relative dei conteggi
espresse in percentuali.
, e a leggere correttamente i valori graficati, per non
incorrere nel rischio di sbagliare di un fattore 100.
I 6 ``istogrammi'' di figura 4.4 mostrano
le frequenze relative dei conteggi
espresse in percentuali.
Figura:
Dati dell'esperienza del contatore a scintillazione.
Diagrammi a barre delle frequenze relative di conteggio.
 |
È da notare come in questo caso
non ha senso in genere mettere delle crocette, poiché
le frequenze relative sono tipicamente numeri razionali.
Per questo motivo questo tipo di rappresentazione grafica
è più propriamente chiamata diagramma a barre.




Next: pzd100Box plot
Up: Descrizione grafica dei dati
Previous: Riduzione dei dati
Indice
Giulio D'Agostini
2001-04-02


![]() 000 eventi ottenuti nelle
stesse condizioni di quelli della tabella 1.2.
000 eventi ottenuti nelle
stesse condizioni di quelli della tabella 1.2.

![]() , e a leggere correttamente i valori graficati, per non
incorrere nel rischio di sbagliare di un fattore 100.
I 6 ``istogrammi'' di figura 4.4 mostrano
le frequenze relative dei conteggi
espresse in percentuali.
, e a leggere correttamente i valori graficati, per non
incorrere nel rischio di sbagliare di un fattore 100.
I 6 ``istogrammi'' di figura 4.4 mostrano
le frequenze relative dei conteggi
espresse in percentuali.
