



Next: Stima dei parametri
Up: Uso di carte logaritmiche
Previous: Carta semilogaritmica
Indice
Proprietà delle carte logaritmiche
La figura 6.6 mostra
un esempio di carta logaritmica.
Possiamo fare delle osservazioni generali che derivano
dalle proprietà dei logaritmi:
- la scala delle
ordinate si infittisce in prossimità di
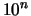 ,
con
,
con  intero
e successivamente si dirada.
Questo è dovuto al fatto che, passando all'ordine
di grandezza successivo, la spaziatura della scala viene
eseguita in unità del nuovo ordine di grandezza. Poiché
questo brusco cambiamento di spaziatura porrebbe problemi
di lettura dei valori, la scala viene successivamente
risuddivisa (questa nuova suddivisione,
presente nelle carte logaritmiche commerciali,
non è riportata in
figura 6.6);
intero
e successivamente si dirada.
Questo è dovuto al fatto che, passando all'ordine
di grandezza successivo, la spaziatura della scala viene
eseguita in unità del nuovo ordine di grandezza. Poiché
questo brusco cambiamento di spaziatura porrebbe problemi
di lettura dei valori, la scala viene successivamente
risuddivisa (questa nuova suddivisione,
presente nelle carte logaritmiche commerciali,
non è riportata in
figura 6.6);
- la distanza fra due punti che differiscono di un certo numeri di
ordini di grandezza è costante. Questo deriva dalle proprietà dei
logaritmi. Infatti, se ad esempio due numeri
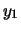 e
e 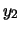 differiscono
di
differiscono
di  ordini di grandezza essi possono essere scritti come
ordini di grandezza essi possono essere scritti come
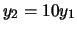 ,
da cui segue che
,
da cui segue che
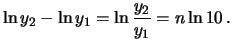 |
(6.20) |
La distanza misurata in centimetri fra due punti che differiscono
di un fattore 10 è pari quindi alla distanza che passa fra
1 e 10, che è pari alla distanza fra 10 e 100 e così via;
- gli intervalli fra potenze di 10 successive si chiamano decadi e, come
detto, sono di lunghezza costante su scala logaritmica. La carta del
nostro di figura 6.6 ha 3 decadi e mezza;
- il valore 0 non può comparire su una scala logaritmica in quanto
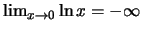 .;
.;
- due rette
che risultano parallele su carta logaritmica differiscono
di una costante per quanto riguarda i valori
delle ascisse,
mentre differiscono per un fattore moltiplicativo
per quanto riguarda le ordinate. Infatti se abbiamo una legge
del tipo
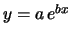 ed effettuiamo una traslazione delle ascisse
di una costante
si ottiene
ed effettuiamo una traslazione delle ascisse
di una costante
si ottiene
- nell'interpolare ad occhio fra le tacche contigue bisogna
prestare attenzione al fatto che la scala non è lineare.
È comunque vero che fra due punti molto vicini l'approssimazione
lineare è abbastanza buona.
È da notare inoltre che, mentre la carta semilogaritmica è stata
introdotta per risolvere problemi legati ad esponenziali (e quindi
a logaritmi naturali), per quanto riguarda
l'uso di carta logaritmica si
è parlato poi di potenze di 10.
Questo è dovuto a due ragioni:
- innanzitutto, da un punto di vista grafico, ciò che è lineare
nel logaritmo naturale è anche lineare nel logaritmo decimale
(si ricordi infatti che
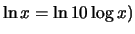 ;
;
- in secondo luogo bisogna notare che l'affermazione fatta precedentemente
secondo cui
``l'ordinata è proporzionale al logaritmo del
valore'' non è perfettamente corretta e lascerebbe presupporre un
assortimento infinito di carte millimetrate a seconda degli ordini di
grandezza di interesse.
Ma poiché su scala logaritmica
passare da un ordine
di grandezza all'altro corrisponde
ad una traslazione, è preferibile disegnare le decadi, lasciando
all'utilizzatore il compito di segnare la potenza di 10 di interesse.
Le carte logaritmiche commerciali
offrono un certo numero di decadi (tipicamente da 2 a 4)
e agli estremi di ogni decade è indicato sempre ``10''.
È lo sperimentatore
a scrivere la successione di potenze adatta a riportare le misure.
Per esempio, nel caso della figura 6.6, se la tensione fosse
stata misurata in Volt si sarebbe riportato sulla scale, da basso verso
l'alto, 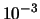 ,
, 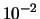 ,
, 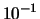 e
e 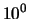 .
.
Un'altra applicazione della carta semilog, oltre a quello di
evidenziare andamenti esponenziali e di valutarne i parametri,
è quello di presentare dati che variano di molti ordini di grandezza.
Questo può essere mostrato dal
confronto del grafico di figura 6.5
con quello di figura 6.6. Mentre su carta lineare
i valori di tensione corrispondenti
a tempi superiori a 14 ms si confondono con lo zero, su
carta semilog tutti i valori hanno lo stesso grado di leggibilità,
nel senso che l'incertezza di lettura
dei valori è in percentuale circa costante
in tutto l'intervallo.
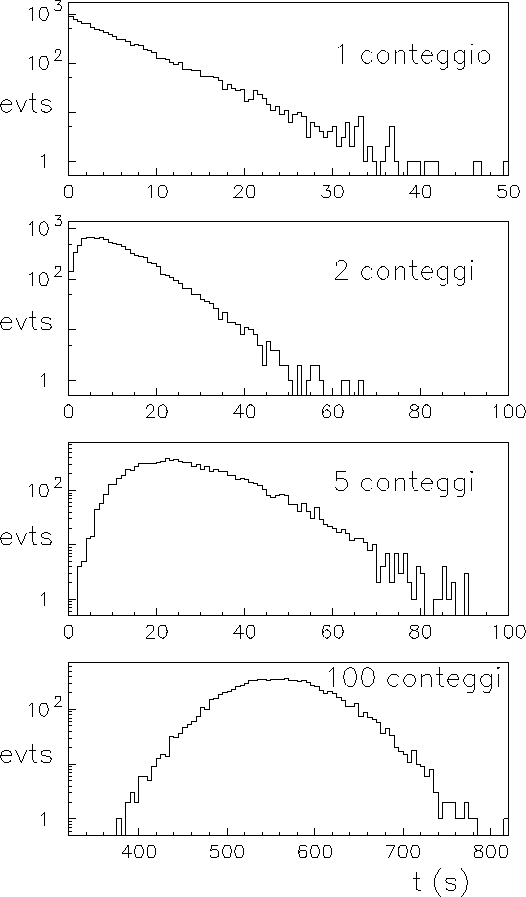
Figura:
Istogrammi dei tempi di attesa per 1, 2, 5 e 100 conteggi
in scala semilog. Si confronti con gli stessi istogrammi in
scala lineare di figura 4.3.
 |
Questa caratteristica della scala è utile non soltanto per
grafici di una grandezza in funzione di un'altra, ma anche
per rappresentare gli istogrammi. In questo caso
vengono evidenziati
piccoli effetti sulle code delle distribuzioni
che è impossibile apprezzare su scala lineare.
Si confrontino per esempio le figure 4.3
e 6.7 dei tempi di attesa per ottenere un certo numero
di conteggi con un contatore a scintillazione. Si notino
in particolare le piccole asimmetrie delle code ancora presenti
per 100 conteggi.




Next: Stima dei parametri
Up: Uso di carte logaritmiche
Previous: Carta semilogaritmica
Indice
Giulio D'Agostini
2001-04-02
