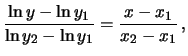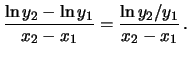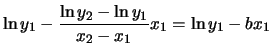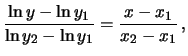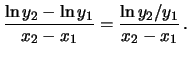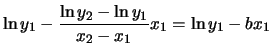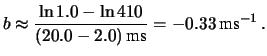Next: Carta doppiologaritmica
Up: Uso di carte logaritmiche
Previous: Proprietà delle carte logaritmiche
Indice
Se i punti hanno un andamento lineare su carta semilog
si può tracciare la retta che meglio si adatta ad essi
e quindi stimare i parametri dell'andamento esponenziale.
Con la notazione di formula 6.15, si può verificare
quanto segue.
- Il parametro
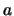 è dato semplicemente dal valore
della
è dato semplicemente dal valore
della 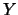 che corrisponde all'intersezione
della retta con l'asse delle ordinate
che corrisponde all'intersezione
della retta con l'asse delle ordinate
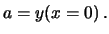 |
(6.22) |
- Il parametro
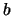 è dato dal coefficiente angolare della
retta. Scegliendo due punti - si ricordi: lontani e ben leggibili -
e utilizando la 6.18 si ottiene, mediante
l'equazione parametrica della retta
è dato dal coefficiente angolare della
retta. Scegliendo due punti - si ricordi: lontani e ben leggibili -
e utilizando la 6.18 si ottiene, mediante
l'equazione parametrica della retta
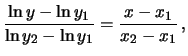 |
(6.23) |
- Nel caso che l'asse delle ordinate (
 ) per motivi di convenienza
non sia riportato nel grafico può essere più comodo
ricavarsi il parametro
) per motivi di convenienza
non sia riportato nel grafico può essere più comodo
ricavarsi il parametro 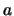 dai due punti della retta:
dai due punti della retta:
(L'alternativa sarebbe di continuare la retta su altri fogli di carta
millimetrata.)
Come esempio numerico stimiamo i parametri dell'andamento
dei dati della tabella 6.2 e delle figure
6.6 e 6.5:
- dal valore della retta per
 si trova
si trova
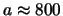 mV.
L'incertezza della lettura della scala è dell'ordine di 10 mV.
Per evitare che, scrivendo 800 mV, si possa pensare di aver
apprezzato anche il secondo zero si può riportare il risultato come
mV.
L'incertezza della lettura della scala è dell'ordine di 10 mV.
Per evitare che, scrivendo 800 mV, si possa pensare di aver
apprezzato anche il secondo zero si può riportare il risultato come
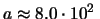 mV, ovvero
mV, ovvero
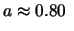
V

- Scegliendo come punti della
retta
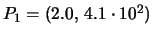 e
e
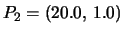 :
A volte questo tipo di esponenziali negativi in funzione
del tempo vengono descritti mettendo all'esponente un parametro
definito positivo che abbia le stesse dimensioni del tempo
e indicato usualmente
:
A volte questo tipo di esponenziali negativi in funzione
del tempo vengono descritti mettendo all'esponente un parametro
definito positivo che abbia le stesse dimensioni del tempo
e indicato usualmente 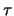 :
Nel nostro caso abbiamo
:
Nel nostro caso abbiamo
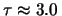 ms.
ms.
- Utilizziamo anche il secondo modo di ricavarci
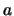 :
:
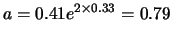
V
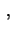
in buon accordo con il valore di 0.80 V ottenuto
con il metodo precedente.




Next: Carta doppiologaritmica
Up: Uso di carte logaritmiche
Previous: Proprietà delle carte logaritmiche
Indice
Giulio D'Agostini
2001-04-02