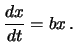Next: Proprietà delle carte logaritmiche
Up: Uso di carte logaritmiche
Previous: Uso di carte logaritmiche
Indice
Tabella:
Misure di tensione durante la scarica di un condensatore.
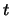 |
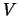 |
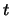 |
 |
| (ms) |
(mV) |
(ms) |
(mV) |
| 2.0 |
411 |
12.0 |
15 |
| 4.0 |
211 |
14.0 |
8 |
| 6.0 |
108 |
16.0 |
4 |
| 8.0 |
56 |
18.0 |
2 |
| 10.0 |
29 |
20.0 |
1 |
|
Figura:
Misure di scarica di un condensatore riportate su carta
lineare.
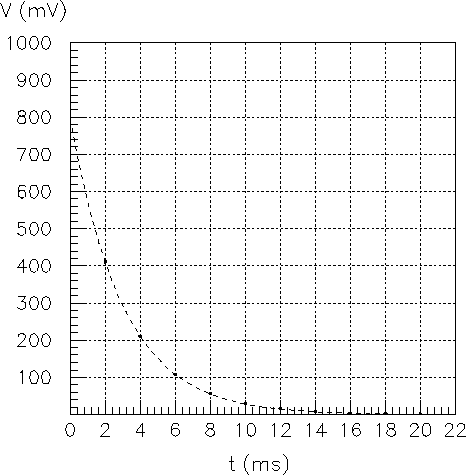 |
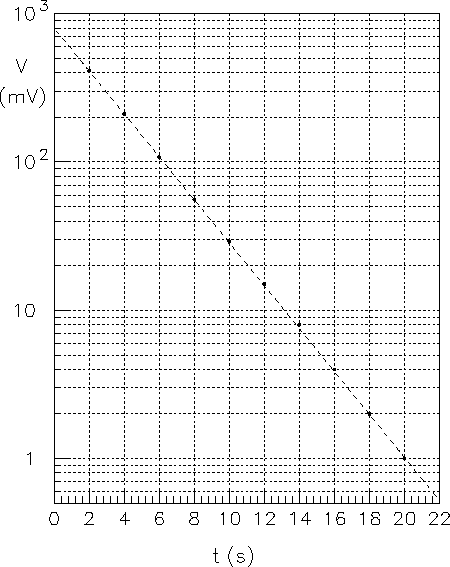
Figura:
Misure di scarica di un condensatore riportate su carta
semilogaritmica.
 |
Supponiamo che due variabili siano legate da una relazione
esponenziale
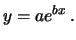 |
(6.15) |
Esempi di fenomeni che seguono tale legge sono: decadimento radioattivo;
accrescimento di colonie di batteri; scambio di calore
di un corpo con l'ambiente circostante; carica e scarica di un condensatore
(un esempio di quest'ultimo è mostrato
nella tabella 6.2
e nella figura 6.5, dove sono riportati i valori di tensione
ai capi del condensatore in funzione del tempo.)
Essi hanno tutti in comune la caratteristica che il tasso istantaneo
di variazione temporale
di una grandezza è proporzionale al valore della grandezza
in quel determinato istante:
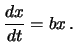 |
(6.16) |
Se dividiamo per 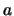 entrambi i membri della (6.15) e
ne prendiamo il logaritmo naturale otteniamo
entrambi i membri della (6.15) e
ne prendiamo il logaritmo naturale otteniamo
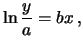 |
(6.17) |
la quale può essere riscritta come
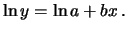 |
(6.18) |
se 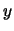 e
e 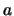 , grandezze omogenee, sono
prese con le stesse unità di misura.
Si ricorda a tale proposito che
gli argomenti di logaritmi ed esponenziale devono essere
adimensionali
e quindi la 6.18 andrebbe più correttamente
scritta come
, grandezze omogenee, sono
prese con le stesse unità di misura.
Si ricorda a tale proposito che
gli argomenti di logaritmi ed esponenziale devono essere
adimensionali
e quindi la 6.18 andrebbe più correttamente
scritta come
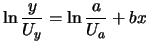 |
(6.19) |
dove con 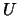 è stata indicata l'unità di misura.
Quindi riportando sulle ascisse i valori della variabile
è stata indicata l'unità di misura.
Quindi riportando sulle ascisse i valori della variabile  e sulle ordinate i valori di
e sulle ordinate i valori di 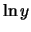 si ottiene un andamento
lineare.
si ottiene un andamento
lineare.
La carta semilogaritmica (o semplicemente
``semilog''), con l'asse delle ordinate proporzionale
al logaritmo del valore, agevola tale compito
in quanto risparmia il calcolo dei logaritmi.




Next: Proprietà delle carte logaritmiche
Up: Uso di carte logaritmiche
Previous: Uso di carte logaritmiche
Indice
Giulio D'Agostini
2001-04-02