| skewness | 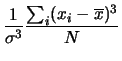 |
(5.36) | |
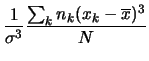 |
(5.37) | ||
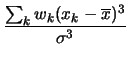 |
(5.38) | ||
| (5.39) |
Per mettere in evidenza eventuali asimmetrie si può utilizzare la media delle potenze dispari degli scarti, con esclusione del primo ordine che sappiamo essere identicamente nulla. Per semplicità si sceglie il cubo degli scarti. Poiché la potenza è maggiore di 1 vuol dire che scarti lontani hanno importanza maggiore ai fini della media. Ne segue che se la media dei cubi degli scarti è positiva significa che la distribuzione ha una coda verso ``destra'' (per valori maggiori della media), se è negativa ha una coda verso sinistra. Per ottenere una misura di asimmetria con la quale poter confrontare distribuzioni che si estendono su ordini di grandezza diversi e che non dipenda dall'unità di misura usata è conveniente esprimere la media dei cubi degli scarti in una unità che sia ``naturale'' per la distribuzione di interesse. Questa scala naturale è scelta essere il cubo della deviazioni standard.
Il cubo degli scarti in unità del cubo della
deviazione standard è chiamato skewness (skew in inglese
significa infatti sbilenco, ma ``sbilenchità''
suona decisamente male5.8...):
| skewness | 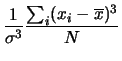 |
(5.36) | |
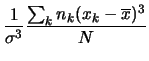 |
(5.37) | ||
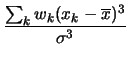 |
(5.38) | ||
| (5.39) |
Svolgiamo i conti in dettaglio per il caso del contatore per ![]() s:
s:
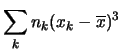 |
|||
L'ultima misura di forma che incontriamo è la curtosi
(in inglese kurtosis). Essa indica l'acutezza della distribuzione,
ovvero
se la forma ricorda più
un ``picco aguzzo'' o una specie di ``altopiano'' (a parte le ovvie
``irregolarità''). Essa è costruita da una media della quarta potenza
degli scarti, opportunamente scalata alla quarta potenza della deviazione
standard:
| curtosi | 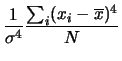 |
(5.40) | |
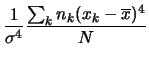 |
(5.41) | ||
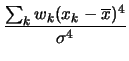 |
(5.42) | ||
| (5.43) |
Per capire l'ordine di grandezza dei valori della curtosi si pensi che se la forma è ``a campana'' regolare (quella della la famosa distribuzione di probabilità gaussiana) la curtosi vale 3; se è piu aguzza si hanno valori maggiori, se più appiattita minori. Si noti invece come il valore della curtosi non dipende dalla larghezza della campana, in quanto il momento quarto è già rapportato alla larghezza misurata dalla deviazione standard.
Un'osservazione più generale è che dalle definizioni si verifica facilmente che sia skewness che curtosi sono invarianti per traslazione e per cambiamenti di scala.
Per il calcolo pratico di ![]() e
e ![]() si utilizzano, in analogia
al caso della varianza, le seguenti
proprietà:
si utilizzano, in analogia
al caso della varianza, le seguenti
proprietà:
| (5.44) | |||
| (5.45) |
La tabella 5.4 riporta la skewness e
la curtosi delle distribuzioni
del contatore mostrate nelle figure 4.2
e 4.3. Per completezza sono state riportate anche
media e deviazione standard. (L'abbondanza delle cifre significative
è giustificata soltanto da esigenze di formattazione dei
valori.) Si vede come l'ultima distribuzione di figura
4.3 ha raggiunto una forma di campana regolare
(curtosi ![]() ).
).
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||