 |
 |
L'estensione a gruppi di ![]() caratteri quantitativi
(grandezze fisiche
nelle nostre applicazioni di laboratorio), chiamati ``n-tuple'',
è abbastanza automatica e quindi ci limitiamo a considerare
il caso bidimensionale e chiamiamo le due grandezze
caratteri quantitativi
(grandezze fisiche
nelle nostre applicazioni di laboratorio), chiamati ``n-tuple'',
è abbastanza automatica e quindi ci limitiamo a considerare
il caso bidimensionale e chiamiamo le due grandezze ![]() e
e ![]() .
.
Per ciascun carattere si possono calcolare tutte le misure di posizione, dispersione e forma che abbiamo incontrato, semplicemente considerandone uno alla volta. Questa operazione corrisponde quindi a proiettare la distribuzione bidimensionale in due distribuzioni unidimensionali.
Ne segue che le suddette misure
di forma unidimensionali non sono sensibili
a caratteristiche legate alla struttura
bidimensionale dei dati. In particolare si perdono le correlazioni
fra le due grandezze, ovvero la preferenza di ![]() ad assumere
certi particolari valori per ciascuno
dei valori della
ad assumere
certi particolari valori per ciascuno
dei valori della ![]() . Ad esempio
se le due città in cui si misura la temperatura sono vicine, o almeno
sullo stesso emisfero, quando è caldo in una farà mediamente
caldo anche nell'altra, e analogalmente per il freddo.
. Ad esempio
se le due città in cui si misura la temperatura sono vicine, o almeno
sullo stesso emisfero, quando è caldo in una farà mediamente
caldo anche nell'altra, e analogalmente per il freddo.
Il modo migliore per studiare le eventuali correlazioni fra i dati
è di osservarli su uno scatter plot o con altra rappresentazione grafica
opportuna (un normale grafico se c'è un solo punto per ogni coppia
di possibili valori [![]() ,
, ![]() ]) e considerare se è ragionevole
che ci sia una dipendenza funzionale fra una grandezza e l'altra.
Questo sarà argomento del capitolo sui cosiddetti fit.
]) e considerare se è ragionevole
che ci sia una dipendenza funzionale fra una grandezza e l'altra.
Questo sarà argomento del capitolo sui cosiddetti fit.
Per ora presentiamo una variabile statistica atta a quantificare il grado di correlazione lineare fra le due grandezze, anche se ne sconsigliamo l'uso a questo livello, specie se non accompagnato da una ispezione grafica della distribuzione bidimensionale.
In analogia alla varianza di una variabile, si definisce la covarianza
come media dei prodotti degli scarti delle due grandezze
rispetto alla media:
| Cov |
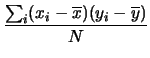 |
(5.46) | |
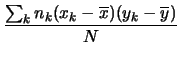 |
(5.47) | ||
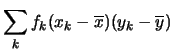 |
(5.48) | ||
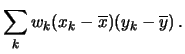 |
(5.49) |
| Cov |
(5.50) |
Se
Cov![]() è positiva vuol dire che quando una delle due grandezze
presenta scarti positivi (rispetto alla media) anche l'altra grandezza
ha mediamente scarti positivi; se una ha scarti negativi anche l'altra
ha mediamente scarti negativi. Se invece la covarianza è negativa
significa che gli scarti si presentano preferibilmente con il segno opposto.
Si dice che nei due casi le grandezze sono (linearmente) correlate
positivamente o negativamente. Se essa è nulla non c'è correlazione
(lineare) fra le due grandezze (ma ci può essere una correlazione
più complicata).
è positiva vuol dire che quando una delle due grandezze
presenta scarti positivi (rispetto alla media) anche l'altra grandezza
ha mediamente scarti positivi; se una ha scarti negativi anche l'altra
ha mediamente scarti negativi. Se invece la covarianza è negativa
significa che gli scarti si presentano preferibilmente con il segno opposto.
Si dice che nei due casi le grandezze sono (linearmente) correlate
positivamente o negativamente. Se essa è nulla non c'è correlazione
(lineare) fra le due grandezze (ma ci può essere una correlazione
più complicata).
Se si prova a calcolare la covarianza su coppie di valori anche scelti a caso raramente si avrà esattamente zero. Va quindi precisato meglio cosa si intende per covarianza ``piccola'' (prossima a zero). Per questo motivo si preferisce una variabile adimensionale, ottenuta dividendo la varianza per le deviazioni standard di ciascuna delle grandezze, prese come unità di scala. Si ottiene così il coefficiente di correlazione:
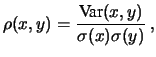 |
(5.51) |
Come per la varianza, skewness e curtosi per il calcolo della covarianza non vengono utilizzate le formule che la definiscono, bensì si fa uso della proprietà
| Cov |
(5.52) |
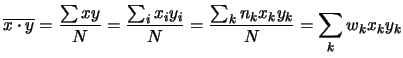 |
(5.53) |
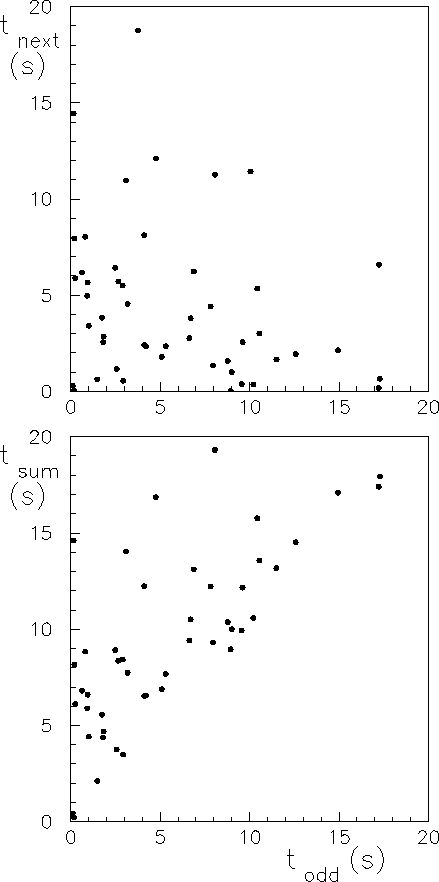
Come esempio di ricerca di correlazioni mostriamo in alto della figura 5.2 lo scatter plot di due tempi di attesa consecutivi registrati al contatore. Non si notano correlazioni al di fuori di quelle che possono essere simulate da fluttuazioni casuali. La figura in basso mostra invece la somma di due tempi di attesa in funzione del primo di essi. In questo caso chiaramente la correlazione è stata forzata ed è infatti visibile nello scatter plot. Il coefficiente di correlazione vale nei due casi rispettivamente -0.24 e +0.63. Si noti come la figura indichi la presenza o assenza di correlazione molto più chiaramente di quanto non si possa evincere dalla differenza (dei moduli) dei due coefficienti di correlazione. In particolare, la correlazione di -0.24 è chiaramente prodotta dai grandi valori dei tempi, i quali sono seguiti o preceduti più frequentemente da numeri piccoli semplicemente perché le combinazioni di due tempi grandi sono più rare e quindi non sono apparse nelle 50 coppie della figura. Ma anche eliminando i punti in cui una delle due coordinate è maggiore di 14s il coefficiente di correlazione resta ancora abbastanza diverso da zero (-0.14).
Quindi, in conclusione, il coefficiente di correlazione misura il grado di correlazione lineare fra due grandezze, ma