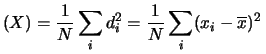Next: Analogia meccanica di media
Up: Misure di dispersione
Previous: Misure di dispersione
Indice
Più la distribuzione è ``larga'' e più
è frequente trovare grandi scarti
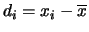 , sia positivi
che negativi. Quindi, come la media può essere utilizzata per
valutare la posizione tipica dei dati sperimentali, così la
media degli scarti potrebbe essere utilizzata come misura della
dispersione dei dati. Ma, poiché gli scarti positivi sono
compensati da scarti negativi, la media degli scarti, presi con il loro segno,
è nulla. Si potrebbe ovviare a questo inconveniente considerando
la media del
modulo degli scarti, ma per comodità
si preferisce
calcolare la media dei quadrati degli scarti e prendere poi
la radice quadrata (positiva). Queste due grandezze sono chiamate
rispettivamente varianza e deviazione standard
(o scarto quadratico medio). I simboli utilizzati in questo
testo
sono Var e
, sia positivi
che negativi. Quindi, come la media può essere utilizzata per
valutare la posizione tipica dei dati sperimentali, così la
media degli scarti potrebbe essere utilizzata come misura della
dispersione dei dati. Ma, poiché gli scarti positivi sono
compensati da scarti negativi, la media degli scarti, presi con il loro segno,
è nulla. Si potrebbe ovviare a questo inconveniente considerando
la media del
modulo degli scarti, ma per comodità
si preferisce
calcolare la media dei quadrati degli scarti e prendere poi
la radice quadrata (positiva). Queste due grandezze sono chiamate
rispettivamente varianza e deviazione standard
(o scarto quadratico medio). I simboli utilizzati in questo
testo
sono Var e 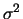 per la varianza,
per la varianza, 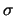 per la deviazione
standard5.6.
Dalla definizione abbiamo quindi
per la deviazione
standard5.6.
Dalla definizione abbiamo quindi
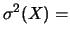 Var Var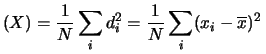 |
(5.11) |
ovvero,
se i dati sono riuniti in classi,
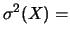 Var Var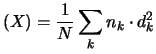 |
 |
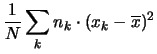 |
(5.12) |
| |
 |
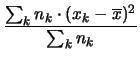 |
(5.13) |
| |
 |
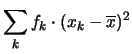 |
(5.14) |
| |
 |
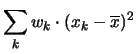 |
(5.15) |
e
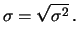 |
(5.16) |
Vedremo nel paragrafo 5.6 il modo
più opportuno per calcolare la varianza.




Next: Analogia meccanica di media
Up: Misure di dispersione
Previous: Misure di dispersione
Indice
Giulio D'Agostini
2001-04-02