



Next: Valutazione pratica della deviazione
Up: Descrizione quantitativa dei dati
Previous: Analogia meccanica di media
Indice
Proprietà di media e varianza
Innanzitutto verifichiamo le proprietà di media e varianza
trovate dalle analogie meccaniche, seguendo lo
stesso ordine dei punti del paragrafo precedente.
- La somma dei quadrati degli scarti rispetto al generico punto
 è pari a
è pari a
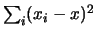 .
Dalla condizione di minimo
.
Dalla condizione di minimo
da cui segue che
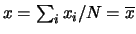 .
.
- Se
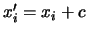 , allora la nuova media sarà
, allora la nuova media sarà
- Analogalmente per la varianza otteniamo
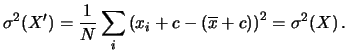 |
(5.25) |
- In modo analogo, è semplice
dimostrare le proprietà di media e deviazione standard per un
cambiamento di scala e viene lasciato come esercizio;
- Infine, la proprietà
Var
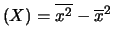 sarà ripresa nel prossimo paragrafo.
sarà ripresa nel prossimo paragrafo.
In generale si ha quindi:
Queste proprietà formali possono essere utili nel fare i conti.
Infatti:
- se si deve calcolare media e deviazione standard di valori in cui
variano soltanto le ultime cifre
(ad esempio: 102.3, 104.8, 111.3, 105.5)
è molto più rapido e sicuro considerare solo le cifre fluttuanti
(nell'esempio riportato
sottraendo 100) e aggiungere la parte costante
alla fine sulla sola media;
- se una grandezza è ottenuta da un'altra mediante una trasformazione
lineare (ad esempio la conversione da tensione a temperatura di una
termocoppia) e sono note media e deviazione standard di una delle
grandezze si ottengono i valori relativi all'altra senza dover rianalizzare
i singoli valori di temperatura.




Next: Valutazione pratica della deviazione
Up: Descrizione quantitativa dei dati
Previous: Analogia meccanica di media
Indice
Giulio D'Agostini
2001-04-02