| (10.7) | |||
| (10.8) |
Ripetendo il ragionamento effettato
al punto 1 del paragrafo 10.4, si può pensare
che le due misure siano fatte in successione temporale (l'ordine non
ha importanza).
Questa volta entriamo però un po'
più in dettaglio. Per generalizzare l'esempio numerico,
indichiamo con
![]() il possibile valore di previsione
di
il possibile valore di previsione
di ![]() che può risultare dopo l'esperimento
che può risultare dopo l'esperimento ![]() -mo. Chiaramente,
prima di fare l'esperimento non possiamo sapere che valore di
-mo. Chiaramente,
prima di fare l'esperimento non possiamo sapere che valore di
![]() si otterrà. Questo è vero anche se ipotizziamo
che
si otterrà. Questo è vero anche se ipotizziamo
che ![]() abbia un valore ben determinato.
Quindi esso può essere considerato un numero
aleatorio con distribuzione densità di probabilità
abbia un valore ben determinato.
Quindi esso può essere considerato un numero
aleatorio con distribuzione densità di probabilità
![]() . Poichè i risultati
espressi dalle (10.7) e (10.8)
hanno il significato di distribuzioni normali di
. Poichè i risultati
espressi dalle (10.7) e (10.8)
hanno il significato di distribuzioni normali di ![]() intorno a
intorno a
![]() , possiamo considerarli equivalenti a
quanto si otterrebbe considerando una prior uniforme su
, possiamo considerarli equivalenti a
quanto si otterrebbe considerando una prior uniforme su ![]() e una verosimiglianza
e una verosimiglianza
![]() normale.
Si tratta, essenzialmente, del ragionamento opposto
di quello del cane-cacciatore usato nelle inversioni
di probabilità. Quindi, indicando con
normale.
Si tratta, essenzialmente, del ragionamento opposto
di quello del cane-cacciatore usato nelle inversioni
di probabilità. Quindi, indicando con ![]() l'incertezza
su
l'incertezza
su ![]() derivante dall'
derivante dall'![]() -ma misura, i risultati
(10.7) e (10.8) equivalenti a
quelli che si sarebbero ottenuti da una verosimiglianza
del tipo
-ma misura, i risultati
(10.7) e (10.8) equivalenti a
quelli che si sarebbero ottenuti da una verosimiglianza
del tipo
Quindi, l'apprendimento sul valore ![]() è equivalente alla seguente
catena di aggiornamento:
è equivalente alla seguente
catena di aggiornamento:
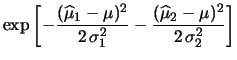 |
(10.9) |
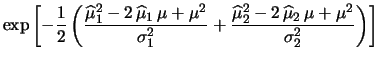 |
![$\displaystyle \exp{\left[-\frac{(\widehat{\mu}_1-\mu)^2}
{2\,\sigma_1^2} -
\frac{(\widehat{\mu}_2-\mu)^2}
{2\,\sigma_2^2}
\right]}$](img1463.png) |
(10.10) | |
![$\displaystyle \exp{\left[-\frac{1}{2}
\left( \frac{\widehat{\mu}^2_1-2\,\wideha...
...c{\widehat{\mu}^2_2-2\,\widehat{\mu}_2\,\mu+\mu^2}
{\sigma_2^2}
\right)\right]}$](img1464.png) |
|||
![$\displaystyle \exp{\left[-\frac{1}{2}
\left( \frac{-2\,(\widehat{\mu}_1\,\sigma...
...,\mu+
(\sigma_1^2+\sigma_2^2)\,\mu^2
}
{\sigma_1^2\,\sigma_2^2}
\right)\right]}$](img1465.png) |
|||
![$\displaystyle \exp{\left[-\frac{1}{2}
\left(\frac{-2\,\overline{x}\,\mu+\mu^2}
{\sigma^2_{\overline{x}}}
\right)\right]}\,,$](img1467.png) |
(10.11) |
| (10.14) |
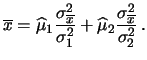 e
e
Le formule che danno
![]() e
e
![]() sono conosciute
come combinazione dei risultati con gli inversi dei quadrati delle
varianze. Si tratta di una media pesata, ove il peso di ogni
``punto sperimentale'' è pari all'inverso della varianza
associata alla sua incertezza. Si noti come il peso della combinazione
dei risultati è pari alla somma dei pesi di ciascun risultato
parziale.
Nel caso dell'esempio numerico con il
quale abbiamo iniziato la discussione abbiamo:
sono conosciute
come combinazione dei risultati con gli inversi dei quadrati delle
varianze. Si tratta di una media pesata, ove il peso di ogni
``punto sperimentale'' è pari all'inverso della varianza
associata alla sua incertezza. Si noti come il peso della combinazione
dei risultati è pari alla somma dei pesi di ciascun risultato
parziale.
Nel caso dell'esempio numerico con il
quale abbiamo iniziato la discussione abbiamo:
| (10.15) |