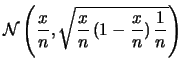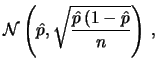Next: Combinazione di più risultati
Up: Misure di conteggio in
Previous: Valutazione parametro della Poissoniana
Indice
Ci possiamo comportare in un modo analogo nell'effettuare
inferenze su parametro 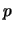 di una binomiale.
Consideriamo in questo caso l'esperienza simulata del pallinometro
a due file di chiodi, in particolare il primo risultato
ottenuto nel bin 0 lanciando 1000 palline (vedi tabella
1.3). Abbiamo ottenuto 254 palline.
Assumiamo di non conoscere i dettagli costruttivi del pallinometro
e che questa sia la sola informazione in nostro possesso.
Cosa possiamo dire sulla probabilità che in un prossimo
lancio fatto nelle stesse condizioni la pallina cada di nuovo
nel bin 0? Intuitivamente diciamo il 25.4%, ma anche
altri (infiniti) valori sono compatibili con i dati sperimentali.
Diciamo che, in ogni caso, sembra fortemente ragionevole
di essere in presenza di un processo descritto da una distribuzione
binomiale avente
di una binomiale.
Consideriamo in questo caso l'esperienza simulata del pallinometro
a due file di chiodi, in particolare il primo risultato
ottenuto nel bin 0 lanciando 1000 palline (vedi tabella
1.3). Abbiamo ottenuto 254 palline.
Assumiamo di non conoscere i dettagli costruttivi del pallinometro
e che questa sia la sola informazione in nostro possesso.
Cosa possiamo dire sulla probabilità che in un prossimo
lancio fatto nelle stesse condizioni la pallina cada di nuovo
nel bin 0? Intuitivamente diciamo il 25.4%, ma anche
altri (infiniti) valori sono compatibili con i dati sperimentali.
Diciamo che, in ogni caso, sembra fortemente ragionevole
di essere in presenza di un processo descritto da una distribuzione
binomiale avente 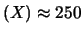 e
e
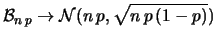 , ovvero
E
, ovvero
E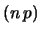 , valore per il quale la
distribuzione è circa normale.
Abbiamo quindi, sulla traccia del caso precedente:
, valore per il quale la
distribuzione è circa normale.
Abbiamo quindi, sulla traccia del caso precedente:
ove, per comodità, abbiamo indicato con 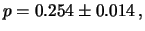 lo
stimatore di
lo
stimatore di 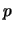 , dato da
, dato da 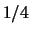 .
Nel caso che stiamo esaminando abbiamo:
compatibile con il valore di
.
Nel caso che stiamo esaminando abbiamo:
compatibile con il valore di 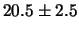 valutato da argomenti di simmetria.
Chiaramente, a questa compatibilità non va dato altro significato
che quello che discende dalle leggi della probailità, ed in particolare
dal teorema di Bernoulli, ovvero che sarebbe stato abbastanza
improbabile osservare un valore di frequenza relativa molto distante
da quello di probabilità. Nel caso in cui noi fossimo stati
veramente in stato di ignoranza sul meccanismo cui cui le palline
scendono saremmo stati disposti ad accettare, come valore di probabilità,
un ampio spettro di valori (al limite, allo stesso modo
tutti quelli fra 0 e 1). Ricordiamo come sia questo stato di indifferenza
rispetto a
valutato da argomenti di simmetria.
Chiaramente, a questa compatibilità non va dato altro significato
che quello che discende dalle leggi della probailità, ed in particolare
dal teorema di Bernoulli, ovvero che sarebbe stato abbastanza
improbabile osservare un valore di frequenza relativa molto distante
da quello di probabilità. Nel caso in cui noi fossimo stati
veramente in stato di ignoranza sul meccanismo cui cui le palline
scendono saremmo stati disposti ad accettare, come valore di probabilità,
un ampio spettro di valori (al limite, allo stesso modo
tutti quelli fra 0 e 1). Ricordiamo come sia questo stato di indifferenza
rispetto a 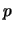 ad autorizzarci ad effettuare le inversioni di probabilità
del tipo cane-cacciatore, che portano alle formule trovate.
ad autorizzarci ad effettuare le inversioni di probabilità
del tipo cane-cacciatore, che portano alle formule trovate.




Next: Combinazione di più risultati
Up: Misure di conteggio in
Previous: Valutazione parametro della Poissoniana
Indice
Giulio D'Agostini
2001-04-02