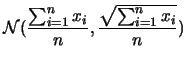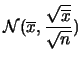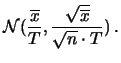Next: Valutazione di di una
Up: Misure di conteggio in
Previous: Misure di conteggio in
Indice
Consideriamo l'esperienza simulata del contatore e concentriamoci
sulla prima misura da 300 s,
la quale ha dato 55 conteggi (vedi paragrafo 1.1
e tabelle 1.1)
Vediamo come sia possibile, da questa sola informazione,
ricavarsi non solo l'intensità del processo di Poisson
(questo è comunque possibile, come l'intuizione suggerisce,
dal numero di conteggi diviso il tempo di misura)
ma anche l'incertezza su tale valore.
Abbiamo già visto come questo può essere
fatto in maniera rigorosa usando
lo schema di inferenza bayesiana (vedi paragrafo
9.8). Possiamo risultare analoghi facendo
il seguente ragionamento:
- dato il tipo di fenomeno fisico, lo possiamo modellizzare
con un fenomeno di Poisson di intensità
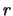 ;
fissando il tempo di misura, i possibili conteggi che saranno osservati
sono descritti da una distribuzione poissoniana di parametro
;
fissando il tempo di misura, i possibili conteggi che saranno osservati
sono descritti da una distribuzione poissoniana di parametro 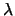 ignota:
ignota:
- essendo il valore misurato
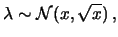 grande, ci aspettiamo che,
molto probabilmente anche
grande, ci aspettiamo che,
molto probabilmente anche 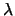 sia grande, ove ``grande''
indica che l'approssimazione della poissoniana con una normale
è abbastanza buona, ovvero:
sia grande, ove ``grande''
indica che l'approssimazione della poissoniana con una normale
è abbastanza buona, ovvero:
- assumendo uno stato di conoscenza a priori su
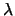 abbastanza vago
possiamo utilizzare l'inversisone di probabilità
del tipo ``cane-cacciatore'':
ottenendo quindi
abbastanza vago
possiamo utilizzare l'inversisone di probabilità
del tipo ``cane-cacciatore'':
ottenendo quindi
Confrontando questo risultato con quello delle figure
9.2 e 9.3, vediamo come
questo risultato sia compatibile con quelli già ottenuti
e di qualità confrontabile a quello ottenuto dal
complesso delle misure da 3 s, ma inferiore a quello
ottenuto da tutte le misure da 300 s.
Vediamo ora come ottenere un risultato che tenga conto di tutte le
misure effettuate ad un certo tempo fissato.
- Le 100 misure da 300 s equivalgono ad una sola misura da 30000,
ovvero:
da cui
- Possiamo generalizzare questo caso al caso generale,
pensando alle
 misure di durate
misure di durate 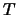 ,
scrivendo:
,
scrivendo:
Si noti inoltre come, quando si hanno molte misure, non è richiesta
l'ipotesi di normalità di ciascuno dei valori osservabili, essendo
sufficiente che essa sia soddisfatta dalla variabile ``somma delle
osservazioni''. Pertanto queste formule
sono applicabile anche all'insieme delle misure
da 3 s. La tabella 10.1
fornisce i risultati che si ottengono per 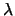 e per
e per
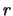 da ciascun gruppo.
da ciascun gruppo.
Tabella:
Risultati si 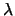 e su
e su 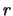 ottenuti dai
dati simulati del contatore.
ottenuti dai
dati simulati del contatore.
| |
|
|
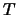 |
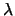 |
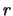 |
| (s) |
(conteggi) |
(conteggi/s) |
| |
|
|
| |
|
|
| 3 |
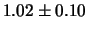 |
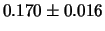 |
| 6 |
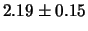 |
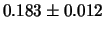 |
| 12 |
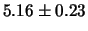 |
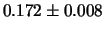 |
| 30 |
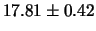 |
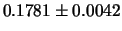 |
| 100 |
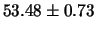 |
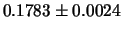 |
| 300 |
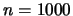 |
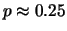 |
| |
|
|
|
Si noti come 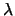 aumenti con il tempo di misura,
mentre
aumenti con il tempo di misura,
mentre 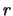 è circa indipendente entro le incertezze.
Inoltre, come era da aspettarsi, la qualità delle misure,
quantificata dalla precisione, aumenta con il tempo di misura.
Un'altra osservazione importante è che l'incertezza sia
stata ricavata soltanto dalle medie, senza tener
conto delle deviazioni standard calcolate in ciascun
gruppetto.
è circa indipendente entro le incertezze.
Inoltre, come era da aspettarsi, la qualità delle misure,
quantificata dalla precisione, aumenta con il tempo di misura.
Un'altra osservazione importante è che l'incertezza sia
stata ricavata soltanto dalle medie, senza tener
conto delle deviazioni standard calcolate in ciascun
gruppetto.




Next: Valutazione di di una
Up: Misure di conteggio in
Previous: Misure di conteggio in
Indice
Giulio D'Agostini
2001-04-02
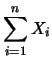
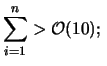
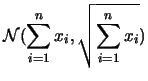 allora:
allora: