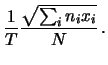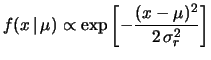Next: Misure dirette con verosimiglianza
Up: pzd100Teorema di Bayes e
Previous: Confronto fra due ipotesi
Indice
Nel caso più generale 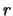 potrebbe assumere, in
principio, un qualsiasi valore reale intero. Associamo
quindi ad essa una variabile casuale continua,
i cui gradi di fiducia sono descritti da una funzione
densità di probabilità
potrebbe assumere, in
principio, un qualsiasi valore reale intero. Associamo
quindi ad essa una variabile casuale continua,
i cui gradi di fiducia sono descritti da una funzione
densità di probabilità 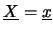 . Applicando
il teorema di Bayes valutiamo il riaggiornamento
dei diversi gradi di fiducia alla luce dei dati
. Applicando
il teorema di Bayes valutiamo il riaggiornamento
dei diversi gradi di fiducia alla luce dei dati
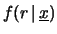 . A parte il solito
fattore di normalizzazione, abbiamo
. A parte il solito
fattore di normalizzazione, abbiamo
Quest'ultimo modo di scrivere il teorema di Bayes
è per rendere più esplicito il ruolo svolto
dalla verosimiglianza
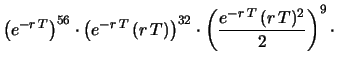 per il riaggiornamento della probabilità.
Per quanto riguarda
per il riaggiornamento della probabilità.
Per quanto riguarda
 , possiamo
pensare sia alla particolare sequenza osservata
(come effettivamente indicato da
, possiamo
pensare sia alla particolare sequenza osservata
(come effettivamente indicato da
 )
o la distribuzione statistica ottenuta
calcolando le frequenze dei diversi conteggi.
Come abbiamo visto nel paragrafo precedente, il risultato
non cambia, in quanto la probabilità delle due
differisce per il fattore multinomiale che,
non dipendendo da
)
o la distribuzione statistica ottenuta
calcolando le frequenze dei diversi conteggi.
Come abbiamo visto nel paragrafo precedente, il risultato
non cambia, in quanto la probabilità delle due
differisce per il fattore multinomiale che,
non dipendendo da 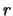 , può essere riassorbita
nella costante di normalizzazione. Scrivendo
le varie probabilità in funzione di
, può essere riassorbita
nella costante di normalizzazione. Scrivendo
le varie probabilità in funzione di 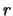 otteniamo:
otteniamo:
dove, dal primo al secondo passaggio abbiamo
eliminato tutti i fattori che non dipendono
da 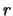 e che quindi possono essere riassorbiti
nella costante di proporzionalità. Inoltre,
alla fine il risultato è stato
riscritto nel modo più
generale introducendo
e che quindi possono essere riassorbiti
nella costante di proporzionalità. Inoltre,
alla fine il risultato è stato
riscritto nel modo più
generale introducendo
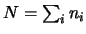 , numero di occorrenze del risultato
di ciascuna misura
e
, numero di occorrenze del risultato
di ciascuna misura
e
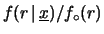 , numero totale di misure.
, numero totale di misure.
Possiamo comunque calcolare
abbastanza facilmente il valore per il quale
tale espressione di
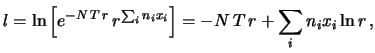 ha un massimo, se usiamo il trucco di
calcolare il massimo del suo logaritmo naturale.
Chiamando quindi
ha un massimo, se usiamo il trucco di
calcolare il massimo del suo logaritmo naturale.
Chiamando quindi
abbiamo che la condizione di minimo è data da
dalla quale si ricava
Il risultato finale è abbastanza semplice:
il valore di 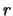 che, in base a questi dati sperimentali,
ha il maggiore aumento di grado di fiducia è
quello corrispondente al numero medio di
conteggi per unità di tempo. È esattamente il concetto
intuitivo di cui abbiamo fatto uso per ricavare il valore
di
che, in base a questi dati sperimentali,
ha il maggiore aumento di grado di fiducia è
quello corrispondente al numero medio di
conteggi per unità di tempo. È esattamente il concetto
intuitivo di cui abbiamo fatto uso per ricavare il valore
di
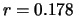 conteggi al secondo dai dati
di 300 s. Applicando questo risultato ai dati da 3 s
otteniamo
conteggi al secondo dai dati
di 300 s. Applicando questo risultato ai dati da 3 s
otteniamo
 conteggi al secondo.
conteggi al secondo.
Terminiamo ricordando che
questi due valori di 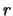 non sono altro
che quelli più favoriti dai due campioni di dati.
Tuttavia anche altri valori, specialmente quelli ``molto prossimi'',
sono supportati dai mdati.
non sono altro
che quelli più favoriti dai due campioni di dati.
Tuttavia anche altri valori, specialmente quelli ``molto prossimi'',
sono supportati dai mdati.
Figura:
Fattore di aggiornamento relativo
(rispetto al massimo)
dell'intensità
del processo di Poisson responsabile dei dati simulati del
contatore. La linea continua si riferisce alle ``misure'' da 300 s,
mentre quella tratteggiata si riferisce a quella da 3 s. Queste
curve hanno la stessa forma della distribuzione di probabilità
di 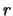 condizionata dall'osservazione dei rispettivi
dati, se si suppone una distribuzione iniziale uniforme
(
condizionata dall'osservazione dei rispettivi
dati, se si suppone una distribuzione iniziale uniforme
(
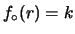 ).
).
 |
La figura 9.2 mostra
il fattore di aggiornamento
relativo (``a.r.'') dei gradi di fiducia rispetto al
massimo nel caso dei due campioni simulati
(la linea continua per le misure da 300 s e quella
tratteggiata per quelle da 3 s).
Si vede come i risultati delle misure da 300 ci
``costringono'' a credere ad un ristretto intervallo
di valori di 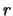 intorno a 0.178, mentre le indicazioni delle misure
da 3 s sono ancora molto più vaghe, nel senso che l'intervallo
di valori ``ragionevolmente possibili'' è più
ampio del caso precedente.
intorno a 0.178, mentre le indicazioni delle misure
da 3 s sono ancora molto più vaghe, nel senso che l'intervallo
di valori ``ragionevolmente possibili'' è più
ampio del caso precedente.
Figura:
Come figura 9.2, ma con fattore
di aggiornamento in scala logaritmica: è evidente
il diverso potere dei due campioni di dati simulati
al fine di discriminare fra i valori più o meno possibili di 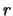 .
.
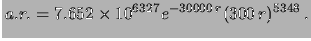 |
Questo si vede ancora meglio dalla figura
9.3, in cui il fattore
relativo di aggiornamento
è mostrato su scala logaritmica.
Si noti che, a questo punto,
il problema inferenziale è risolto,
almeno dal punto di vista concettuale.
Le figure 9.2 e
9.3 mostrano nel modo più
``oggettivo'' le informazioni estraibili dai dati
per quanto riguarda 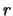 . Se il nostro stato di
conoscenza su
. Se il nostro stato di
conoscenza su 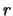 fosse stato tale da ammettere
tutti i valori nello stesso modo (ovvero
fosse stato tale da ammettere
tutti i valori nello stesso modo (ovvero
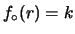 )
le curve di queste figure, opportunamente normalizzate,
ci danno direttamente le distribuzioni di probabilità
di
)
le curve di queste figure, opportunamente normalizzate,
ci danno direttamente le distribuzioni di probabilità
di 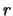 . Essenzialmente, quello che vedremo nella parte
di inferenza statistica applicata alle incertezze di misura
sarà come valutare in modo approssimato forma
e parametri delle distribuzioni (valore atteso e
deviazione standard). Ad esempio, la curva
del fattore di aggiornamento relativo ottenuta
da 300 s sembra fortemente gaussiana, anche
se la forma esatta della funzione non è affatto
banale, essendo infatti:
. Essenzialmente, quello che vedremo nella parte
di inferenza statistica applicata alle incertezze di misura
sarà come valutare in modo approssimato forma
e parametri delle distribuzioni (valore atteso e
deviazione standard). Ad esempio, la curva
del fattore di aggiornamento relativo ottenuta
da 300 s sembra fortemente gaussiana, anche
se la forma esatta della funzione non è affatto
banale, essendo infatti:
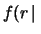 |
(9.13) |
Assumendo una funzione iniziale uniforme, la funzione finale
differisce dalla (9.13) soltanto per un fattore
di normalizzazione:
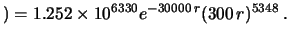 dati 300 s dati 300 s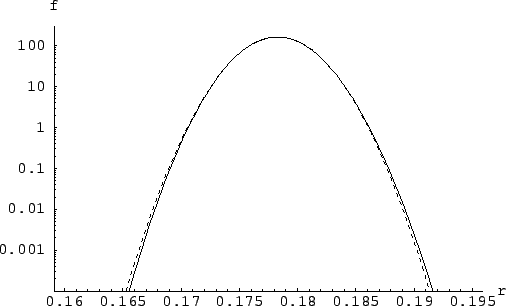 |
(9.14) |
Questa funzione è rappresentata dalla curva continua di figura
9.4.
Figura:
Funzione densità di probabilità di 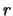 ottenuta
dalle misure di 300 s assumendo una distribuzione iniziale uniforme.
La linea solida è data dalla (9.13 opportunamente
normalizzata. Quella tratteggiata
è ottenuta dall'approssimazione gaussiana.
ottenuta
dalle misure di 300 s assumendo una distribuzione iniziale uniforme.
La linea solida è data dalla (9.13 opportunamente
normalizzata. Quella tratteggiata
è ottenuta dall'approssimazione gaussiana.
 |
Valore atteso e deviazione standard di  sono:
sono:
Il valore atteso è uguale a quello che si ottiene
applicando la (9.12), ovvero esso corrisponde
con il valore per il quale i dati sperimentali suggeriscono
il massimo aumento di grado di fiducia.
La linea tratteggiata di figura 9.4 mostra
una distribuzione gaussiana di valore medio 0.1783 e
deviazione standard 0.0024. L'approssimazione è spettacolare
su diversi ordini di grandezza. Questa osservazione suggerisce
un metodo approssimativo per ricavarsi la deviazione standard
di 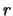 , alla stessa stregua di come ne è stato ricavato il
valore atteso in modo approssimativo. Se
, alla stessa stregua di come ne è stato ricavato il
valore atteso in modo approssimativo. Se
![$\displaystyle f(r) \propto e^{-N\,T\,r}\,r^{\sum_in_ix_i}\,, \sim \propto \exp{\left[-\frac{(r-\mu_r)^2}{2\,\sigma_r}\right]}\,,$](img1296.png) |
(9.17) |
allora, poiché vale per la gaussiana
possiamo imporre le stesse condizioni sulla
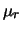 per ricavarci
per ricavarci 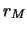 e
e 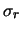 . Il valore atteso
. Il valore atteso 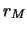 corrisponde a
corrisponde a 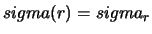 di (9.12). Lasciando il calcolo di
di (9.12). Lasciando il calcolo di
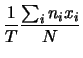 per esercizio, riportiamo insieme il risultato:
per esercizio, riportiamo insieme il risultato:
Applicate al caso delle 100 misure da 300 s, queste formule
danno gli stessi risultati ottenuti facendo esplicitamente
gli integrali.
Nel caso di una sola misura abbiamo:
Questo è un risultato molto interessante. Nelle misure
di conteggio
non abbiamo bisogno di ripetere le osservazioni per ottenere la
deviazione standard associata all'incertezza del
risultato. Sono sufficienti il numero di conteggi e
l'ipotesi sul processo seguito dai conteggi.
Nel seguito utilizzeremo soltanto il metodo approssimato,
che rigiustificheremo mediente il ragionamento del cane
e del cacciatore.




Next: Misure dirette con verosimiglianza
Up: pzd100Teorema di Bayes e
Previous: Confronto fra due ipotesi
Indice
Giulio D'Agostini
2001-04-02
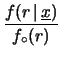
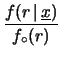
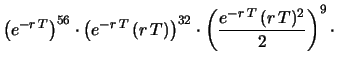 per il riaggiornamento della probabilità.
Per quanto riguarda
per il riaggiornamento della probabilità.
Per quanto riguarda
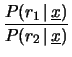 , possiamo
pensare sia alla particolare sequenza osservata
(come effettivamente indicato da
, possiamo
pensare sia alla particolare sequenza osservata
(come effettivamente indicato da
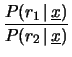 )
o la distribuzione statistica ottenuta
calcolando le frequenze dei diversi conteggi.
Come abbiamo visto nel paragrafo precedente, il risultato
non cambia, in quanto la probabilità delle due
differisce per il fattore multinomiale che,
non dipendendo da
)
o la distribuzione statistica ottenuta
calcolando le frequenze dei diversi conteggi.
Come abbiamo visto nel paragrafo precedente, il risultato
non cambia, in quanto la probabilità delle due
differisce per il fattore multinomiale che,
non dipendendo da 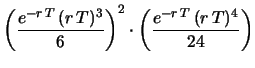
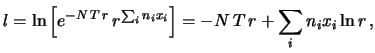 ha un massimo, se usiamo il trucco di
calcolare il massimo del suo logaritmo naturale.
Chiamando quindi
ha un massimo, se usiamo il trucco di
calcolare il massimo del suo logaritmo naturale.
Chiamando quindi
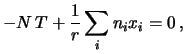
 conteggi al secondo.
conteggi al secondo.
![]() non sono altro
che quelli più favoriti dai due campioni di dati.
Tuttavia anche altri valori, specialmente quelli ``molto prossimi'',
sono supportati dai mdati.
non sono altro
che quelli più favoriti dai due campioni di dati.
Tuttavia anche altri valori, specialmente quelli ``molto prossimi'',
sono supportati dai mdati.

![]() . Se il nostro stato di
conoscenza su
. Se il nostro stato di
conoscenza su ![]() fosse stato tale da ammettere
tutti i valori nello stesso modo (ovvero
fosse stato tale da ammettere
tutti i valori nello stesso modo (ovvero
![]() )
le curve di queste figure, opportunamente normalizzate,
ci danno direttamente le distribuzioni di probabilità
di
)
le curve di queste figure, opportunamente normalizzate,
ci danno direttamente le distribuzioni di probabilità
di ![]() . Essenzialmente, quello che vedremo nella parte
di inferenza statistica applicata alle incertezze di misura
sarà come valutare in modo approssimato forma
e parametri delle distribuzioni (valore atteso e
deviazione standard). Ad esempio, la curva
del fattore di aggiornamento relativo ottenuta
da 300 s sembra fortemente gaussiana, anche
se la forma esatta della funzione non è affatto
banale, essendo infatti:
. Essenzialmente, quello che vedremo nella parte
di inferenza statistica applicata alle incertezze di misura
sarà come valutare in modo approssimato forma
e parametri delle distribuzioni (valore atteso e
deviazione standard). Ad esempio, la curva
del fattore di aggiornamento relativo ottenuta
da 300 s sembra fortemente gaussiana, anche
se la forma esatta della funzione non è affatto
banale, essendo infatti:
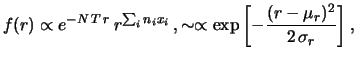
![]() , alla stessa stregua di come ne è stato ricavato il
valore atteso in modo approssimativo. Se
, alla stessa stregua di come ne è stato ricavato il
valore atteso in modo approssimativo. Se
![$\displaystyle f(r) \propto e^{-N\,T\,r}\,r^{\sum_in_ix_i}\,, \sim \propto \exp{\left[-\frac{(r-\mu_r)^2}{2\,\sigma_r}\right]}\,,$](img1296.png)
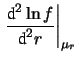
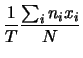 per esercizio, riportiamo insieme il risultato:
per esercizio, riportiamo insieme il risultato: