



Next: Classe continua di ipotesi
Up: pzd100Teorema di Bayes e
Previous: pzd100Teorema di Bayes e
Indice
Supponiamo che, in base alla nostra conoscenza,
le intensità del processo
di Poisson
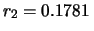 s e
s e
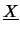 s
siano ugualmente probabili (ad esempio
alla luce dei dati da 300 s che indicano
s
siano ugualmente probabili (ad esempio
alla luce dei dati da 300 s che indicano 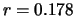 conteggi/s).
A quale dei due crederemo di più qualora
osservassimo la sequenza misurata?
Per compattare la notazione, indichiamo con il
vettore (o ``n-tupla'')
conteggi/s).
A quale dei due crederemo di più qualora
osservassimo la sequenza misurata?
Per compattare la notazione, indichiamo con il
vettore (o ``n-tupla'')
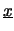 le possibili sequenze osservabili
e con
le possibili sequenze osservabili
e con
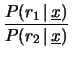 la particolare sequenza che ci
interessa.
Applicando il teorema di Bayes nella forma che
intervenire il rapporto delle verosimiglianze
(il cosiddetto fattore di Bayes), abbiamo:
la particolare sequenza che ci
interessa.
Applicando il teorema di Bayes nella forma che
intervenire il rapporto delle verosimiglianze
(il cosiddetto fattore di Bayes), abbiamo:
ove il fattore 1 deriva
dall'equiprobabilità iniziale delle ipotesi.
Si noti inoltre come saremmo arrivati
alla stessa conclusione se, invece di considerare la probabilità
della sequenza particolare, avessimo considerato
la probabilità della distribuzione costituita da
56 volte zero conteggi, 32 volte un conteggio, 9 volte due conteggi,
2 volte tre conteggi e 1 volta quattro conteggi.
Infatti le due verosimiglianze differiscono per lo
stesso coefficiente
multinomiale (che vale
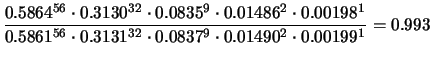 in questo caso),
il quale non dipende da
in questo caso),
il quale non dipende da 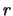 e quindi si semplifica.
Calcolando le probabilità
che entrano nella (9.6), otteniamo il seguente
rapporto di probabilità:
e quindi si semplifica.
Calcolando le probabilità
che entrano nella (9.6), otteniamo il seguente
rapporto di probabilità:
I dati simulati da 3 secondi favoriscono quindi,
anche se molto leggermente, il valore 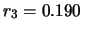 .
Se invece si confrontasse l'ipotesi
.
Se invece si confrontasse l'ipotesi
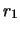 conteggi/s contro
conteggi/s contro 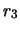 si otterebbe
(sembre assumendo
si otterebbe
(sembre assumendo 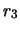 e
e 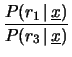 ugualmente possibili a priori):
ugualmente possibili a priori):
ovvero quei dati simulati favoriscono abbastanza
la terza ipotesi.
Prima di procedere al caso più generale di un numero
infinito di ipotesi, vale la pena di fare un commento
su alcuni errori tipici che si commettono quando si parla
di probabilità di dati sperimentali e di probabilità
di ipotesi.
- Innanzitutto bisigna fare attenzione a quando si parla di
probabilità dei dati sperimentali. Essendo dati osservati,
su di essi non c'è incertezza, e quindi la probabilità
vale 1. Scrivere quindi, nel linguaggio che stiamo utilizzando,
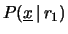 si riferisce, ``genericamente'',
alla probabilità
di osservare quella configurazione di dati sotto quella precisa ipotesi.
si riferisce, ``genericamente'',
alla probabilità
di osservare quella configurazione di dati sotto quella precisa ipotesi.
- Quando si parla di probabilità dei dati sperimentali data una certa ipotesi
si può intendere ``probabilità della particolare sequenza'' o
``probabilità del tipo di distribuzione a cui tale sequenza può
dare luogo''. Come abbiamo visto nel paragrafo precedente,
la differenza fra i due numeri può essere enorme
(
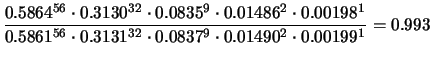 nel caso che stiamo trattando), anche se
per quanto riguarda l'inferenza tale fattore, dovuto al coefficiente
multinomiale binomiale, si semplifica.
nel caso che stiamo trattando), anche se
per quanto riguarda l'inferenza tale fattore, dovuto al coefficiente
multinomiale binomiale, si semplifica.
- La probabilità di avere la sequenza
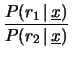 vale,
per le tre ipotesi di
vale,
per le tre ipotesi di 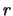 ,
,
ma non possiamo affermare, ad esempio,
``la probabilità che la sequenza
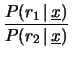 sia
dovuta a
sia
dovuta a 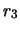 è uguale a
è uguale a
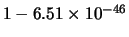 '', perché
altrimenti ci sarebbe una probabilità di
'', perché
altrimenti ci sarebbe una probabilità di
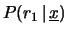 che tale sequenza
non sia dovuta a
che tale sequenza
non sia dovuta a 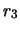 .
Infatti ``esser dovuto a
.
Infatti ``esser dovuto a 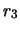 '' ha lo stesso significato
di ``il processo di Poisson di intensità
'' ha lo stesso significato
di ``il processo di Poisson di intensità 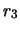 è la causa
della sequenza
è la causa
della sequenza
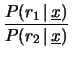 ''. Quindi,
``la probabilità che la sequenza
''. Quindi,
``la probabilità che la sequenza
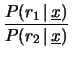 sia dovuta a
sia dovuta a 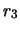 '' è pari a
'' è pari a
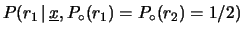 .
È invece corretto dire ``c'è una probabilità di
.
È invece corretto dire ``c'è una probabilità di
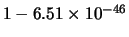 che un processo di Poisson di intensità
che un processo di Poisson di intensità
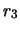 dia luogo alla (produca la) sequenza
dia luogo alla (produca la) sequenza
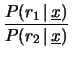 ''.
''.
- Per calcolare la probabilità delle ipotesi bisogna
passare necessariamente attraverso il teorema di Bayes
e quindi attraverso le cosiddette ``prior''.
Quindi, scrivendo esplicitamente
le probabilità iniziali nel condizionante, possiamo avere
i seguenti casi:
Nel caso si stia affrontando un problema controverso e non ce se
la sente di inserire delle probabilità a priori
(necessariamente soggettive e,
se il problema è controverso, per definizione fortemente
dipendenti da persona a persona), la lista delle verosimiglianze
per tutte le ipotesi di interesse rappresenta il modo più oggettivo
di riportare il risultato
dell'esperimento.9.6




Next: Classe continua di ipotesi
Up: pzd100Teorema di Bayes e
Previous: pzd100Teorema di Bayes e
Indice
Giulio D'Agostini
2001-04-02
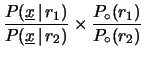
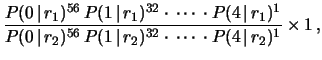
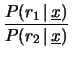 la particolare sequenza che ci
interessa.
Applicando il teorema di Bayes nella forma che
intervenire il rapporto delle verosimiglianze
(il cosiddetto fattore di Bayes), abbiamo:
la particolare sequenza che ci
interessa.
Applicando il teorema di Bayes nella forma che
intervenire il rapporto delle verosimiglianze
(il cosiddetto fattore di Bayes), abbiamo:
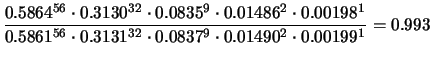 in questo caso),
il quale non dipende da
in questo caso),
il quale non dipende da 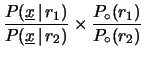
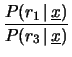 ugualmente possibili a priori):
ugualmente possibili a priori):
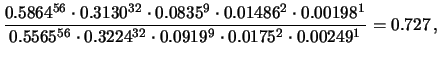
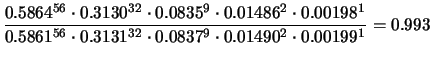 nel caso che stiamo trattando), anche se
per quanto riguarda l'inferenza tale fattore, dovuto al coefficiente
multinomiale binomiale, si semplifica.
nel caso che stiamo trattando), anche se
per quanto riguarda l'inferenza tale fattore, dovuto al coefficiente
multinomiale binomiale, si semplifica.
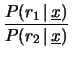 vale,
per le tre ipotesi di
vale,
per le tre ipotesi di 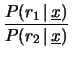 sia
dovuta a
sia
dovuta a 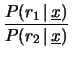 ''. Quindi,
``la probabilità che la sequenza
''. Quindi,
``la probabilità che la sequenza
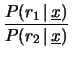 sia dovuta a
sia dovuta a 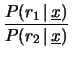 ''.
''.