



Next: Misure indirette ed errori
Up: Misure dirette con verosimiglianza
Previous: Combinazione di più risultati
Indice
- Quali dei risultati non segue la convenzione standard
per le cifre significative?
a)
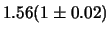 ;
;
b)
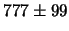 ;
;
c)
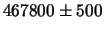 ;
;
d)
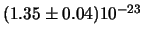 ;
;
e)
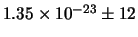 ;
;
f)
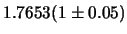 ;
;
g)
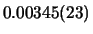 ;
;
h)
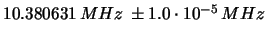 ;
;
i)
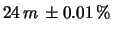 ;
;
l)
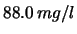 ;
;
m)
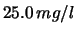 ;
;
- Da rilevamenti su un grande numero di pozzi
risulta che il residuo fisso dell'acqua ha un valore medio
di
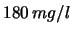 , con una deviazione standard di
, con una deviazione standard di
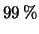 .
Quanto vale la probabilità che un pozzo abbia
l'acqua con un residuo fisso maggiore di
.
Quanto vale la probabilità che un pozzo abbia
l'acqua con un residuo fisso maggiore di
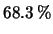 ?
?
- La media aritmetica e la deviazione standard di
una certa grandezza, misurata in unità arbitrarie su un
campione di 10 elementi, valgono rispettivamente
142.9876192 e
24.06595568 (valori letti sul display del calcolatore).
Quanto vale l'intervallo di fiducia, al
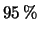 C.L.,
della media della popolazione? Di quanto varia l'intervallo
di fiducia se la stessa media e la stessa
deviazione standard fossero state ottenute da 5 valori?
C.L.,
della media della popolazione? Di quanto varia l'intervallo
di fiducia se la stessa media e la stessa
deviazione standard fossero state ottenute da 5 valori?
- Per misurare il tempo necessario per una certa reazione,
uno sperimentatore esegue, nelle stesse condizioni,
4 misurazioni. I valori ottenuti, espressi in secondi, sono
13.5, 14.2, 10.8, 13.1. Esprimere il risultato non
incertezza al
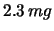 e al
e al 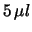 .
.
- Delle prove effettuate su una bilancia con dei pesi campione
hanno mostrato che essa ben tarata
e che i risultati delle singole pesate si distribuiscono intorno al
valore nominale con una deviazione standard di
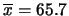 ,
indipendentemente dal peso dell'oggetto. Vengono pesati tre oggetti,
il primo una sola volta e gli altri due più volte. Si ottengono i
seguenti campioni di valori, espressi in grammi:
{20.0045}; {0.8721, 0.8732, 0.8703};
{
0.0137, 0.0138, 0.0166, 0.0153, 0.0170,
0.0168, 0.0160, 0.0107, 0.0163, 0.0185,
0.0139, 0.0135, 0.0143, 0.0154, 0.0171
}.
Dare il risultato delle tre misure con incertezza al
,
indipendentemente dal peso dell'oggetto. Vengono pesati tre oggetti,
il primo una sola volta e gli altri due più volte. Si ottengono i
seguenti campioni di valori, espressi in grammi:
{20.0045}; {0.8721, 0.8732, 0.8703};
{
0.0137, 0.0138, 0.0166, 0.0153, 0.0170,
0.0168, 0.0160, 0.0107, 0.0163, 0.0185,
0.0139, 0.0135, 0.0143, 0.0154, 0.0171
}.
Dare il risultato delle tre misure con incertezza al 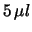 .
Qual'è la misura più precisa?
.
Qual'è la misura più precisa?
- Sui dati dell'esercizio precedente: come saranno dati invece
i risultati se la deviazione standard non è nota?
Considerare
anche il caso in cui si possa ipotizzare una deviazione standard ignota
ma indipendente dalla misura e confrontarlo con il caso in
cui non vale questa ipotesi.
- Osservando
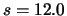 di sangue al microscopio si notano 52 cellule di un certo tipo.
Quanto vale, al
di sangue al microscopio si notano 52 cellule di un certo tipo.
Quanto vale, al 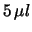 di probabilità la concentrazione media
di tali cellule nel sangue? (Ignorare l'incertezza sul volume).
di probabilità la concentrazione media
di tali cellule nel sangue? (Ignorare l'incertezza sul volume).
- Vengono effettuate 8 misure di conteggio, i cui risultati
si presentano circa poissoniani. La media e la deviazione
standard calcolata sul campione valgono rispettivamente:
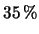 e
e 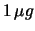 . Calcolare la migliore
stima della media teorica della distribuzione, fornendo il
risultato ad un livello di confidenza del
. Calcolare la migliore
stima della media teorica della distribuzione, fornendo il
risultato ad un livello di confidenza del 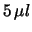 .
.
- Si vuole determinare l'efficienza di un farmaco per far guarire da una
certa malattia. Lo si prova su 357 persone e, di queste, 84
guariscono entro due settimane, mentre su un campione di controllo
molto più grande di quello di test nessuna è guarita. a) Quanto vale, al
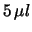 e al
e al 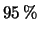 l'efficienza del farmaco?
l'efficienza del farmaco?
b) Quanto deve essere grande il campione se si vuole conoscere l'efficienza
con un'incertezza inferiore a 0.002 al 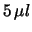 C.L.?
C.L.?
c) Un secondo farmaco, provato su 96 persone affette dalla stessa
malattia, ne fa guarire 31 nello stesso tempo. Quanto vale
da differenza fra l'efficienza del secondo farmaco e quella del primo?
- Si vuole organizzare per le elezioni comunali di una grande città
un ``exit poll'' anonimo per stimare i risultati
delle elezioni prima dello spoglio finale.
Assumiamo di aver scelto i seggi in maniera appropriata al fine
di avere un campione che rifletta in media le caratteristiche
dell'intera popolazione. Su quante persone va effettuato il
sondaggio per ottenere, al livello di confidenza del
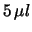 ,
incertezze sui risultati al di sotto di un punto percentuale
per tutti i partiti che ottengano fra il 10 e il
,
incertezze sui risultati al di sotto di un punto percentuale
per tutti i partiti che ottengano fra il 10 e il 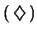 dei suffragi?
dei suffragi?
- Secondo la prima legge di Mendel sull'ereditarietà,
se si incrociano individui che presentano un carattere
dominante e provenienti da una linea pura ( ovvero
sono omozigoti ) con individui anch'essi provenienti da una
linea pura, ma che presenta il carattere recessivo,
si otterrano tutti individui eventi il carattere dominante.
Mendel effettuò 19939 incroci fra diversi caratteri
dei piselli ( vedi es. 4 del capitolo 12 ), ottenendo
tutti caratteri dominanti.
Basandosi soltanto sui risultati
di questi esperimenti,
cosa si può dire circa la probabilità che in un incrocio la legge di
Mendel sia violata?
- In uno degli esperimenti, Mendel incrociò piselli dai semi
rugosi con piselli dai semi lisci, con entrambe le varietà
provenienti da linee pure. Il risultato fu quello di avere
tutti piselli dai semi lisci. Successivamente, nella seconda
generazione, lasciò che le piante si autofecondassero
ed ottenne 5474 casi di semi lisci e 1850 casi di semi rugosi.
Quanto vale la probabilità di
avere un individuo dal carattere dominante
nella seconda generazione?
Utilizzando i limiti dell'intervallo di confidenza trovato,
dare il risultato anche in termini del rapporto fra
frequenza del carattere dominante e frequenza del carattere recessivo.
- Di una grandezza fisica introdotta da un gruppo di teorici
si sa che essa, per definizione,
deve avere un valore compreso fra -1 e 1 (unità arbitrarie).
Al di là del valore accurato della grandezza, difficile da misurare,
è molto importante
per la comunità dei fisici sapere almeno se
essa è minore di -0.5, maggiore di 0.5 o prossima a zero, per
implicazioni su altre teorie.
Un esperimento, progettato per determinare il valore di tale grandezza,
è in grado di fornire un valore misurato distribuito
intorno al valore vero secondo una normale con deviazione standard
0.20. Dopo anni di lavoro e complicate analisi si trova il valore
di 0.75. Quanto vale la probabilità che il valore della grandezza fisica
sia maggiore di 0.5? Determinare anche il limite inferiore al
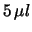 .
.
- Si vuole misurare la radioattività di una certa stanza
mediante l'uso di un contatore Geiger, esprimendo il risultato
in conteggi al secondo. In due minuti si misurano
2250 conteggi.
a) Quanto vale il livello di radioattività al 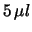 ?
?
b)Il giorno dopo viene effettuata una sola misura di 1 minuto,
ottenendo 1021 conteggi. Cosa si può dire
sulla variazione del livello di radioattività?
- Un campione di sostanza di
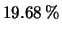 è osservato al microscopio.
In esso si trovano 171 particelle di impurità. Supponendo
che queste particelle si presentano sempre a gruppi di 3,
stimare quanto vale la concentrazione di impurità nel materiale,
fornendo il risultato al
è osservato al microscopio.
In esso si trovano 171 particelle di impurità. Supponendo
che queste particelle si presentano sempre a gruppi di 3,
stimare quanto vale la concentrazione di impurità nel materiale,
fornendo il risultato al 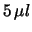 C.L..
C.L..
-
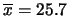 Un giornale effettua un
sondaggio preelettorale su un campione
di 437 persone. Sulla tabella che riporta i risultati
si legge che il
Un giornale effettua un
sondaggio preelettorale su un campione
di 437 persone. Sulla tabella che riporta i risultati
si legge che il 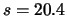 degli elettori voterebbe il partito A.
Supponiamo che il sondaggio sia stato effettuato su un
campione significativo della popolazione.
Quale sarebbe la maniera più corretta
di presentare in risultato?
degli elettori voterebbe il partito A.
Supponiamo che il sondaggio sia stato effettuato su un
campione significativo della popolazione.
Quale sarebbe la maniera più corretta
di presentare in risultato?
-
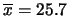 Viene eseguita una serie di 150 misure, ottenendo
Viene eseguita una serie di 150 misure, ottenendo
 e
e 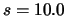 . Quanto vale la probabilità
che, eseguendo un'altra serie di 150 misure sulla stessa grandezza
fisica e nelle stesse condizioni,
la media aritmetica sia
maggiore o uguale di 27.4 ?
. Quanto vale la probabilità
che, eseguendo un'altra serie di 150 misure sulla stessa grandezza
fisica e nelle stesse condizioni,
la media aritmetica sia
maggiore o uguale di 27.4 ?
-
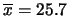 Sui dati del problema precedente: quanto vale invece la probabilità
che una singola misura dia un risultato maggiore o uguale
di 27.4?
Sui dati del problema precedente: quanto vale invece la probabilità
che una singola misura dia un risultato maggiore o uguale
di 27.4?
-
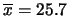 Viene eseguita una serie di 100 misure, ottenendo
Viene eseguita una serie di 100 misure, ottenendo
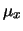 e
e 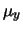 . Quanto vale la probabilità
che eseguendo un'altra serie di 100 misure sulla stessa grandezza
fisica e nelle stesse condizioni
la media aritmetica sia compresa nell'intervallo [-1.4, 1.4]?
. Quanto vale la probabilità
che eseguendo un'altra serie di 100 misure sulla stessa grandezza
fisica e nelle stesse condizioni
la media aritmetica sia compresa nell'intervallo [-1.4, 1.4]?
-
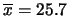 Un campione di sangue è osservato al microscopio e si
osservano 72 paricelle di un certo tipo. Quanto vale la probabilità di
contare, in altro campione di sangue proveniente soggetto
ed osservato nelle stesse condizioni, un numero di particelle
maggiore di 84?
Un campione di sangue è osservato al microscopio e si
osservano 72 paricelle di un certo tipo. Quanto vale la probabilità di
contare, in altro campione di sangue proveniente soggetto
ed osservato nelle stesse condizioni, un numero di particelle
maggiore di 84?
- Si utilizza un contatore per misurare il numero di decadimenti
per unità di tempo
di una sorgente radioattiva.
Si hanno a disposizione 6400 secondi per effettuare la misura.
Discutere se, al fine del calcolo dell'incertezza
sulla quantità da misurare,
è preferibile basarsi sul numero di conteggi totali registrati nei
6400 secondi, oppure è meglio
utilizzare la distribuzione dei conteggi
ottenuta in 100 intervalli di 64 secondi ciascuno.




Next: Misure indirette ed errori
Up: Misure dirette con verosimiglianza
Previous: Combinazione di più risultati
Indice
Giulio D'Agostini
2001-04-02