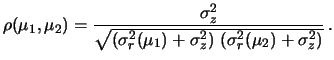Next: Valutazione pratica di dovuto
Up: Misure indirette ed errori
Previous: Calibrazione, intercalibrazione e ``randomizzazione''
Indice
A questo punto, avendo introdotto nel paragrafo
11.2.4
il concetto di correlazione
fra valori di grandezze fisiche
che hanno incertezze comuni e avendo
mostrato la loro importanza nelle inferenze successive,
introduciamo il
coefficiente di correlazione11.5.
Esso è indicato con
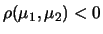 , può avere valori compresi
fra -1 e 1 ed è atto a misurare il
grado di correlazione
(lineare11.6)
fra le due grandezze. Il concetto intuitivo
(nell'applicazione alle misure) è il seguente
, può avere valori compresi
fra -1 e 1 ed è atto a misurare il
grado di correlazione
(lineare11.6)
fra le due grandezze. Il concetto intuitivo
(nell'applicazione alle misure) è il seguente
-
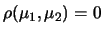 sta ad indicare che,
se il valore vero
sta ad indicare che,
se il valore vero 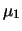 è
maggiore di quello stimato,
anche il valore vero
è
maggiore di quello stimato,
anche il valore vero
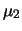 è maggiore del corrispondente
valore stimato;
è maggiore del corrispondente
valore stimato;
- se
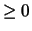 , ad una sovrastima di una grandezza
corrisponde una sottostima dell'altra;
, ad una sovrastima di una grandezza
corrisponde una sottostima dell'altra;
- se
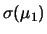 , sovrastime e sottostime dei due valori
sono indipendenti.
, sovrastime e sottostime dei due valori
sono indipendenti.
È chiaro quindi che, nel caso di errori di zero e di scala,
il coefficiente di correlazione fra due grandezze misurate
direttamente con lo
stesso strumento può essere soltanto 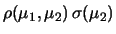 : tutti i valori
saranno eventualmente mal determinati
nello stesso verso.
: tutti i valori
saranno eventualmente mal determinati
nello stesso verso.
Per quanto riguarda l'entità delle possibili sovrastime
e sottostime,
si può dimostrare che esse sono misurate in termini della
deviazione standard:
se 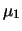 è sovrastimato di
è sovrastimato di 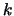 volte
volte
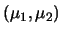 ,
allora
,
allora 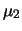 è sovrastimato di
è sovrastimato di 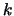 volte
volte
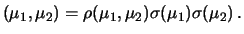 .
.
Spesso si fa uso anche di
un'altra grandezza per quantificare le correlazioni, sebbene in
modo molto meno immediatamente percepibile.
Essa è la covarianza,
indicata con
Cov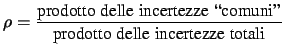 e legata al coefficiente
di correlazione da
e legata al coefficiente
di correlazione da
Cov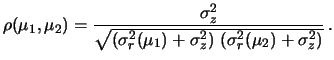 |
(11.23) |
Si noti come la covarianza abbia dimensioni che
sono il prodotto delle dimensioni
delle due grandezze. Per questo è difficile dal suo valore farsi un'idea
intuitiva dell'entità delle correlazioni.
Subsections




Next: Valutazione pratica di dovuto
Up: Misure indirette ed errori
Previous: Calibrazione, intercalibrazione e ``randomizzazione''
Indice
Giulio D'Agostini
2001-04-02
è sovrastimato di
volte
, allora
è sovrastimato di
volte
.
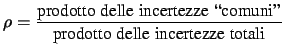 e legata al coefficiente
di correlazione da
e legata al coefficiente
di correlazione da