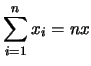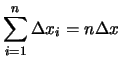Next: Regola della mezza divisione
Up: Critica della ``teoria degli
Previous: Critica della ``teoria degli
Indice
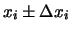
Questa espressione starebbe a significare che
-
- se siamo ``praticamente certi'' che il valore vero
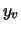 è compreso nell'intervallo dato da
è compreso nell'intervallo dato da
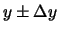 ,
ne segue che siamo ``praticamente certi'' che il valore vero
di
,
ne segue che siamo ``praticamente certi'' che il valore vero
di 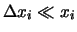 è compreso nell'intervallo dato da
è compreso nell'intervallo dato da
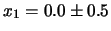 .
.
È opinione comune che, affinché la formula sia valida,
debba valere
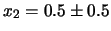 (giustificazione usuale).
Se accettiamo per buona tale espressione di ``propagazione
lineare degli errori massimi'' e i presupposti
sui quali essa si basa andiamo incontro ad incongruenze,
come mostrano gli esempi che seguono.
(giustificazione usuale).
Se accettiamo per buona tale espressione di ``propagazione
lineare degli errori massimi'' e i presupposti
sui quali essa si basa andiamo incontro ad incongruenze,
come mostrano gli esempi che seguono.
- Se
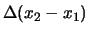 e
e
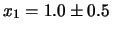 quanto vale
quanto vale
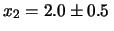 ?
(La seconda condizione non è più valida.)
?
(La seconda condizione non è più valida.)
- Misuriamo due spessorini, uno di 1 mm e l'altro di 2 mm
(valori ``esatti''),
con un righello aventi divisioni di 1 mm.
Otteniamo
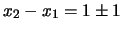 mm e
mm e
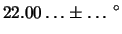 mm,
da cui
mm,
da cui
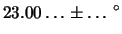 mm. Come si recita in questi casi, le
due misure sono ``uguali entro gli errori''. Ciò nonostante,
una qualsiasi ispezione visuale suggerisce che uno spessore è
circa il doppio dell'altro.
Nessuno potrà giurare che il rapporto
fra i due sia esattamente 2: potrebbe essere 1.8, 1.9, 2.0, 2.1, 2.2,
o forse 1.7 o 2.3, ma sicuramente sono esclusi i valori prossimi
a 1.
Si ottiene quindi un risultato formale in netta contraddizione
con quanto si crede: una conclusione paradossale!
mm. Come si recita in questi casi, le
due misure sono ``uguali entro gli errori''. Ciò nonostante,
una qualsiasi ispezione visuale suggerisce che uno spessore è
circa il doppio dell'altro.
Nessuno potrà giurare che il rapporto
fra i due sia esattamente 2: potrebbe essere 1.8, 1.9, 2.0, 2.1, 2.2,
o forse 1.7 o 2.3, ma sicuramente sono esclusi i valori prossimi
a 1.
Si ottiene quindi un risultato formale in netta contraddizione
con quanto si crede: una conclusione paradossale!
- Consideriamo un termometro a mercurio, avente divisioni di 0.1
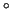 C
e di cui
sappiamo che potrebbe essere scalibrato al più di
0.6
C
e di cui
sappiamo che potrebbe essere scalibrato al più di
0.6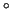 C. Consideriamo le seguenti letture, lasciando sospese
le incertezze e le successive elaborazioni:
C. Consideriamo le seguenti letture, lasciando sospese
le incertezze e le successive elaborazioni:
La risposta usuale a questo quesito è che
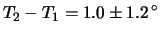 e
e
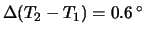 sono pari a 0.6
sono pari a 0.6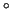 C, mentre
C, mentre
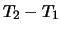
C

(Qualcuno, sospettando un tranello, azzarda un
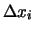 C.)
Non è difficile convincersi che, mentre incertezze
di 0.6
C.)
Non è difficile convincersi che, mentre incertezze
di 0.6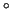 C su ciascuna
misura sono ragionevoli, se intese come ``errori massimi'',
quella sulla differenza non
è affatto sensata. La calibrazione assoluta non può avere
alcun effetto sulla differenza fra valori di temperatura così
prossimi. Alla luce delle considerazioni del punto precedente,
possiamo affermare che la stima più ragionevole dell'incertezza
su
C su ciascuna
misura sono ragionevoli, se intese come ``errori massimi'',
quella sulla differenza non
è affatto sensata. La calibrazione assoluta non può avere
alcun effetto sulla differenza fra valori di temperatura così
prossimi. Alla luce delle considerazioni del punto precedente,
possiamo affermare che la stima più ragionevole dell'incertezza
su 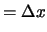 sia inferiore a 0.1
sia inferiore a 0.1 C (per arrivare ad
valore numerico bisognerà premettere altre considerazioni e
saperne di più sul termometro,
sulle condizioni di misura e su
chi ha eseguito le letture).
C (per arrivare ad
valore numerico bisognerà premettere altre considerazioni e
saperne di più sul termometro,
sulle condizioni di misura e su
chi ha eseguito le letture).
- Torniamo ora all'espressione ``praticamente sicuri'':
- -
- cosa significa?
- -
- cosa si paga se non è vero (se dovesse risultare che il valore
vero è al di fuori dell'intervallo indicato, o almeno
``molto al di fuori'', visto che non si trattava
di certezza assoluta)?
- -
- è quello che serve veramente?
Analizziamo quest'ultimo punto.
Prendiamo, come esempio, la somma
di tante grandezze di uguale valore e incertezza
(tanto per semplificare i conti):
La somma degli
 valori e la sua incertezza, calcolata usando
la (A.1), sono
valori e la sua incertezza, calcolata usando
la (A.1), sono
Confrontiamo questo
risultato con quanto si ottiene mediante un piccolo
programma di simulazioneA.1,
assumendo che il valore vero delle 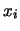 potrebbe essere
in qualsiasi punto entro l'intervallo
potrebbe essere
in qualsiasi punto entro l'intervallo
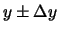 .
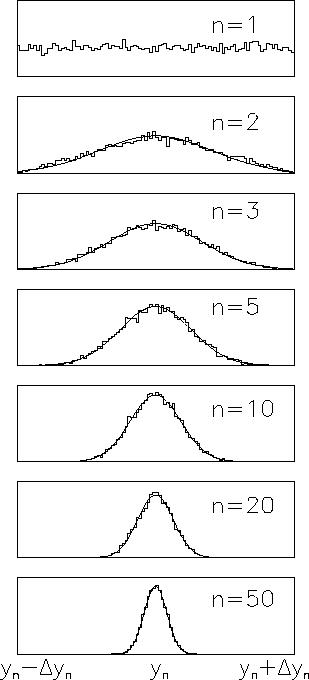
La figura A.1
mostra i risultati di 10000 simulazioni, per n=1,
2, 3, 5, 10, 20 e 50.
.
La figura A.1
mostra i risultati di 10000 simulazioni, per n=1,
2, 3, 5, 10, 20 e 50.
Figura:
Simulazione della distribuzione del
valore vero ottenuta sommando  risultati
aventi gli stessi limiti di errore. Per confronto
viene anche riportata la distribuzione normale
avente come media il centro dell'intervallo e
deviazione standard
risultati
aventi gli stessi limiti di errore. Per confronto
viene anche riportata la distribuzione normale
avente come media il centro dell'intervallo e
deviazione standard
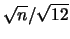 (vedi appendice
sul teorema del limite centrale).
(vedi appendice
sul teorema del limite centrale).
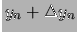 |
Per comodità l'asse delle ascisse
è preso fra
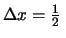 e
e
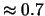 dati dalla
formula precedente.
Come si vede dalla figura,
è senz'altro corretto affermare di essere ``praticamente
certi'' che il risultato sia in quell'intervallo, ma,
al crescere di
dati dalla
formula precedente.
Come si vede dalla figura,
è senz'altro corretto affermare di essere ``praticamente
certi'' che il risultato sia in quell'intervallo, ma,
al crescere di  ,
la prudenza è tale che il risultato si è ``impoverito''
rispetto alle sue potenzialità originarie.
,
la prudenza è tale che il risultato si è ``impoverito''
rispetto alle sue potenzialità originarie.
Si potrebbe obiettare che in pratica si fanno solo poche misure.
Questo può essere vero in una semplice esperienza di laboratorio,
ma nel mondo reale la propagazione delle incertezze è
in principio illimitata: ognuno utilizza informazioni precedentemente
ricavate da lui o da altri, e le conclusioni verranno utilizzate
da altri ancora, etc. (nessuno fa una misura per incorniciare il
risultato a casa, senza nessuna influenza per
altriA.2...).
Riassumendo, possiamo affermare che l'uso della
cosiddetta
``teoria'' degli errori massimi conduce a
- una tendenza a sovrastimare le incertezze;
- all'impossibilità di trattare propriamente gli effetti
delle correlazioni.
Ora, qualcuno potrebbe pensare che l'effetto delle correlazioni
possa essere una finezza e che la sovrastima delle incertezze
sia da ritenere addirittura
essere un pregio. Se gli esempi precedenti, che hanno mostrato
come facilmente si arriva a sovrastime di un ordine di grandezza
non dovesse bastare, citiamo la Guida ISO in proposito:
``The method [quello raccomandato dalla Guida]
stands, therefore, in contrast
to certain older methods that have the following two ideas in common:
- The first idea is that the uncertainty reported should be 'safe'
or 'conservative' (...) In fact, because the evaluation
of the uncertainty of a measurement result is problematic,
it was often made deliberately large.
- ...
(...) if the 'maximum error bound'
(the largest conceivable deviation from the putative best estimate)
is used (...) the resulting uncertainty (...) will be
unusable by anyone wishing to incorporate it into subsequent calculations
(...)''.
Comunque, il motivo principale per cui vanno evitate le sovrastime
delle incertezze è che in questo caso è più facile
arrivare a
risultati in accordo (artificiosamente) con
valori noti o con quelli di altri esperimenti. Questo impedisce
di identificare i possibili effetti sistematici che possono distorcere
il risultato
(si ricordi che spesso dietro gli errori sistematici
c'è quasi sempre della Fisica: dispersioni termiche, rumore
elettromagnetico, approssimazioni rozze, etc.),
o di scoprire addirittura una nuova fenomenologia
(ma questo non capita nelle esperienze di laboratorio didattico...).
Aumentare artificiosamente le incertezze equivale a rifiutarsi
di imparare. Farlo per ``paura di sbagliare'' è
puerileA.3.




Next: Regola della mezza divisione
Up: Critica della ``teoria degli
Previous: Critica della ``teoria degli
Indice
Giulio D'Agostini
2001-04-02