Cause delle incertezze di misura

Passiamo ora ad elencare le possibili sorgenti di incertezza di misura seguendo lo stesso ordine delle raccomandazioni ISO. Essa rappresenta una sorta di ``decalogo'' da scorrere ogni volta che si cercano le possibili sorgenti di errore.

1. Incompleta definizione del misurando.
   Ad esempio la ``percentuale di potassio nell'acqua del Mar Adriatico'' non definisce completamente il misurando e il risultato può dipendere da dove è prelevato il campione. Lo stesso vale per l'``accelerazione di gravità al livello del mare'', in quanto essa dipende anche dalla latitudine e, potendo eseguire la misura con precisione infinita, dal punto esatto (quale è il livello del mare?). Si capisce quindi come ogni indeterminazione sulla definizione si riflette su una infinità di valori che soddisfano la definizione (vedi definizione del valore vero^8.9). Nel paragrafo 11.9 sarà trattato numericamente il caso di ``densità dell'aria''.

2. Imperfetta realizzazione della definizione del misurando.
   ``Vita media di decadimento dell'isotopo $X$'' e ``sezione efficace di un neutrone bombardato da un fascio di elettroni'' sono definizioni univoche, almeno in linea di principio. In pratica non è facile ottenere un campione assolutamente puro di sostanza o effettuare delle misure nelle condizioni ideali della definizione.

   Per fare altri esempi, si pensi a: ``accelerazione di un corpo lungo un piano inclinato privo di attrito'' e ``periodo di un pendolo semplice di lunghezza $l$''. Qui si fa chiaramente riferimento ad astrazioni di cui gli apparati sperimentali sono imperfette realizzazioni.

3. Campione non rappresentativo, ovvero il campione misurato non rappresenta il misurando definito
   Caso classico sono i sondaggi per stimare - misurare - la ``percentuale della popolazione in possesso di un certo carattere'' (in senso lato). Non avendo a disposizione le risorse economiche e il tempo per eseguire un'indagine adeguata, o in mancanza di un modello teorico per la scelta del campione si rischia di effettuare un sondaggio su coloro che sono caratterizzati da un'altra proprietà comune dalla quale può dipendere il carattere oggetto della ricerca (ad esempio si può rischiare di intervistare solo amici o concittadini, o solo coloro che vedono la televisione ad una certa ora o che trascorrono il pomeriggio a casa). Altro esempio è quello dell'analisi chimico-fisica di un quadro che comporta la distruzione di un campione di tela. Le informazioni che si ricavano da un lembo periferico - più facilmente ottenibile per l'analisi - possono differire da quelle ottenibili da parti artisticamente più interessanti del quadro (convincereste il Louvre a cedervi un occhio della Gioconda?).

   Figura: Esempio di errore sistematico dovuto all'utilizzo di uno strumento a temperatura diversa da quella nominale.

   

4. Imperfetta conoscenza delle condizioni ambientali di influenza o inadeguata conoscenza degli effetti di tali condizioni
   Ad esempio una misura di precisione può essere falsata dalla non esatta conoscenza della temperatura ambientale. La figura 8.3 mostra, ad esempio, l'errore introdotto nella misura, se questa viene eseguita ad una temperatura $T$ diversa da quella di riferimento $T_\circ$. Conoscendo i coefficienti di dilatazione termica è possibile correggere il valore ottenuto (come mostrato in figura), ma ogni eventuale incertezza sul valore di $T$ (e, in misura minore, su $\alpha$) si ``propaga'' nell'incertezza sulla lunghezza $l$.
5. Errore di lettura di uno strumento.
   La lettura delle scale analogiche dipende dall'acuità visiva e dall'abilità di stima dello sperimentatore. Ad esempio, un errore grossolano è quello di parallasse, mostrato in figura 8.4.

   Figura: Errore di parallasse. La figura mostra la diversa lettura che si ottiene osservando la scala dello strumento da angolazioni diverse. Gli strumenti di precisione hanno una porzione della scala riflettente allo scopo di minimizzare tale effetto.

   
   È da notare inoltre che la qualità delle interpolazioni della lettura dipendono molto dalle condizioni di lavoro (illuminazione e facilità di lettura) e dal fatto che la grandezza fisica sia statica o rapidamente variabile con il tempo. Non è inoltre da trascurare la dipendenza dall'importanza che lo sperimentatore dà a priori alla qualità della determinazione di tale grandezza fisica. Infatti è inutile sforzarsi a leggere i decimi di millimetro per dare al falegname le dimensioni di una finestra.

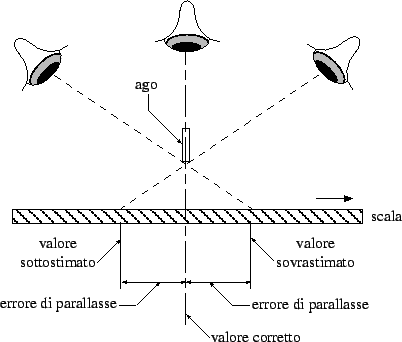   Da queste considerazioni ne segue che l'incertezza da associare all'errore di misura non è univocamente determinata dal tipo di strumento (ved, ad esempio, l'esperienza descritta nel paragrafo 2.2).

   Figura: Capacità di interpolazione fra le tacche. Distribuzione della deviazione standard della differenza fra il valore stimato e quello letto sul nonio. I risultati sono basati sulle misure eseguite da 25 studenti, ciascuno dei quali ha effettuato 10 letture.

   

6. Risoluzione finita o soglia di discriminazione dello strumento.
   Ad esempio, se la lettura avviene con uno strumento digitale si è limitati alla cifra meno significatica del display anche se la qualità del segnale di misura è tale da essere significativamente sensibile a variazioni di valori ben minori dell'entità dell'ultima cifra del display.
   Come esempio numerico prendiamo un dispositivo elettronico che produce una variazione nella tensione di uscita di 17 mV se la pressione cambia di 1 mbar Assumiamo che a 1018 mbar il segnale di misura sia pari a 3.714 V, direttamente convertito in mbar e mostrato su un display digitale a 4 cifre. Una variazione di $\pm 0.2$ mbar non produce nessuna variazione dell'indicazione (``1018'') pur causando una variazione di $\pm 3.4$ mV sul segnale di misura (per i concetti di risoluzione di strumenti analogici e di soglia di discriminazione vedi par. 8.9.1).
7. Valori inesatti dei campioni e dei materiali di riferimento.
   Si pensi ad esempio ad una massa campione con graffi, polvere e ossidazioni, oppure ad una soluzione campione di pH che si è contaminata dal momento della sua preparazione.

   I campioni servono a calibrare (o ricalibrare) gli strumenti. Ogni incertezza sul valore del campione si riflette sulla costante di calibrazione e quindi su tutte le misure che saranno eseguite con tale strumento. Le incertezze su queste misure saranno quindi correlate.

8. Valore inesatto di costanti e altri parametri che intervengono nell'analisi dei dati.
   Spesso le misure indirette dipendono da costanti e parametri misurati dallo stesso sperimentatore, da suoi colleghi o semplicemente riportate su articoli o libri. Ogni incertezza su queste grandezze si propaga su quelle misurate.

9. Approssimazioni e assunzioni che intervengono nel metodo e nella procedura di misura.
   Ad esempio, nel modello teorico elementare che descrive l'oscillazione del pendolo sono usualmente trascurati gli effetti che derivano dal fatto che l'angolo di oscillazione è diverso da zero. Se si conoscono i termini correttivi si può ottenere, in linea di principio, il valore $T(\alpha=0)$ dal valore misurato $T(\alpha=\alpha_\circ)$. Se invece si è coscienti di effetti che non si è in grado di calcolare, oppure se si può effettuare soltanto una stima grossolana degli stessi, allora si dovrà introdurre un ulteriore contributo all'incertezza.
10. Variazioni in osservazioni ripetute del misurando sotto condizioni di misura apparentemente identiche.
    Queste variazioni sono legate ai cosiddetti errori casuali, dei quali parleremo in modo più particolareggiato nel seguito.

La determinazione quantitativa delle incertezze verrà trattata in modo sistematico nel seguito. Per ora, restando su un piano più qualitativo, è importante notare che:

• non è facile effettuare una suddivisione netta fra le diverse sorgenti di incertezza e, in particolare, tutte quelle dei punti 1-9 hanno una qualche influenza sul punto 10 in quanto difficilmente esse produrranno esattamente un identico effetto durante una serie di misure;
• nella maggior parte delle misure lo sperimentatore fa parte integrante del processo di misura. Il risultato dipende molto da abilità ed esperienza di chi effettua le misure, sia per quanto riguarda la manualità nell'operare gli strumenti nella lettura di strumenti analogici, che per la capacità di vagliare i vari contributi all'errore di misura. Quindi è difficile separare l'incertezza ``intrinseca'' dovuta allo strumento da quella di altri contributi.