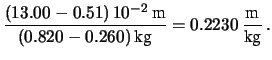 kg kg |
|||
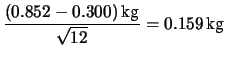 kg kg |
|||
Si noti l'altissima correlazione negativa fra i due parametri: detto alla buona, è un po' come se, invece di aver misurato 2 grandezze (nel senso di 2 grandezze indipendenti), ne avessimo misurate 1.04.
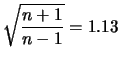 m m |
|||
L'accordo è più che soddisfacente12.5
Tralasciando il coefficiente di correlazione si sarebbe ottenuto
Si noti infine come l'effetto dovuto al termine
di correlazione sia ancora più importante per valori
all'interno della distribuzione dei punti sperimentali,
con un massimo nel baricentro.12.7
Per una massa di 0.576kg si
prevede un allungamento di
![]() mm (che diventerebbe
mm (che diventerebbe ![]() omettendo le correlazioni).
omettendo le correlazioni).
- le letture degli allungamenti sono state effettuate su
un foglio di carta millimetrata solidale con il supporto
della molla: deviazioni dell'indicazione dell'ordine di grandezza
di
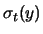 mm o maggiori sono impensabili;
mm o maggiori sono impensabili;
- i pesetti sono stati misurati tutti insieme, per sottrazione
rispetto alla tara, e quindi qualsiasi loro combinazione
ha un'incertezza standard ben inferiore ad una parte su mille;
anche un'eventuale incertezza di 1 g, proprio a voler
esagerare, sulla massa iniziale
(
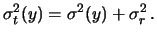 ), che si riflette su tutti i valori di massa
e va perciò considerata come un errore di zero, produce al più
un'incertezza sull'intercetta di 0.2mm; infine, le eventuali
differenze12.8fra un pesetto e l'altro sono già incluse,
indirettamente, in
), che si riflette su tutti i valori di massa
e va perciò considerata come un errore di zero, produce al più
un'incertezza sull'intercetta di 0.2mm; infine, le eventuali
differenze12.8fra un pesetto e l'altro sono già incluse,
indirettamente, in 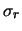 .
.
- Abbiamo indicato con
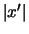 la deviazione standard
che quantifica l'incertezza della previsione del valore
(``vero'') di
la deviazione standard
che quantifica l'incertezza della previsione del valore
(``vero'') di 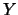 , per un dato valore di
, per un dato valore di 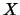 .
Come abbiamo visto, questa incertezza è minima in corrispondenza
del baricentro dei punti sperimentali e aumenta quando ci
si allontana da esso.
.
Come abbiamo visto, questa incertezza è minima in corrispondenza
del baricentro dei punti sperimentali e aumenta quando ci
si allontana da esso.
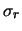 è dovuta invece alle fluttuazioni attese del
singolo valore misurato intorno all'andamento medio
dei punti sperimentali. Si sarebbe tentati di dire che
essa misura le fluttuazioni dei valori delle
è dovuta invece alle fluttuazioni attese del
singolo valore misurato intorno all'andamento medio
dei punti sperimentali. Si sarebbe tentati di dire che
essa misura le fluttuazioni dei valori delle 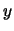 letti
avendo fissato
letti
avendo fissato 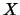 , ma in realtà essa tiene conto anche
delle piccole fluttuazioni del valore di
, ma in realtà essa tiene conto anche
delle piccole fluttuazioni del valore di 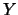 da un valore di
da un valore di 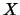 all'altro.
all'altro.
- C'è infine un'ultima deviazione standard, che chiamiamo
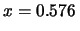 che tiene conto della combinazione dei due effetti.
Essa risponde alla domanda: ``che valori di
che tiene conto della combinazione dei due effetti.
Essa risponde alla domanda: ``che valori di 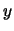 potrei osservare
se facessi l'esperimento fissando il valore di
potrei osservare
se facessi l'esperimento fissando il valore di  ?''.
L'incertezza sui parametri si riflette sul valore vero di
?''.
L'incertezza sui parametri si riflette sul valore vero di 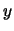 ed inoltre la singola misura ha un'ulteriore incertezza
intorno al valore di
ed inoltre la singola misura ha un'ulteriore incertezza
intorno al valore di 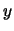 medio. Si può dimostrare
che queste due incertezze si combinano, come al solito,
quadraticamente:
medio. Si può dimostrare
che queste due incertezze si combinano, come al solito,
quadraticamente:
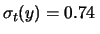
(12.26)