



Next: Cifre significative dei parametri
Up: Analisi grafiche
Previous: Grafici
Indice
Grafici lineari: stima grafica dei parametri
della retta
Figura:
Grafici dell'allungamento in funzione della massa applicata
alla molla
e del suo periodo di oscillazione in funzione della radice quadrata
della massa. I cerchietti indicano i punti
utilizzati per il calcolo dei parametri della retta.
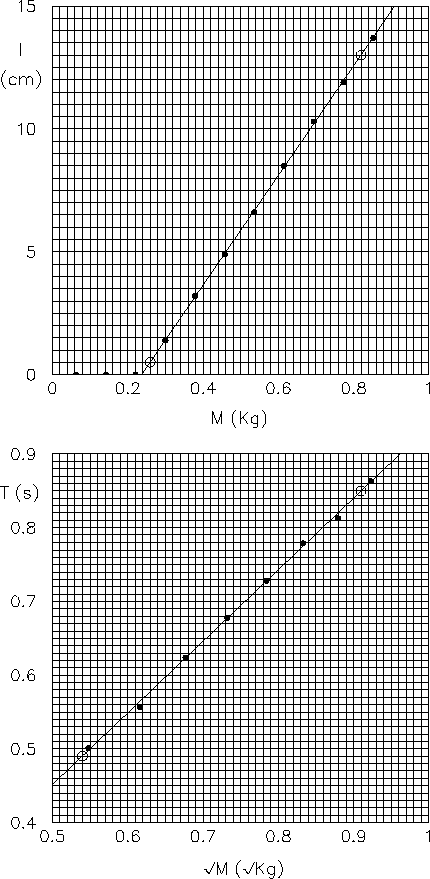 |
La figura 6.3 mostra i dati della prima serie
di misure di tabella 2.5 riportati su opportuni grafici.
Il primo grafico mostra l'allungamento, espresso in centimentri,
in funzione
della massa applicata espressa in chilogrammi. Il secondo mostra invece
il periodo di oscillazione, espresso in secondi, in
funzione della radice quadrata della massa applicata espressa
in unità di radice quadrata di chilogrammo.
Entrambi i grafici mostrano, al di sopra di una massa critica,
un andamente lineare dei punti. Questo indica che le relazioni
(2.1) e (2.2) sono
ragionevolmente soddisfatte. È quindi possibile
tracciare la retta che meglio passa per i punti,
determinando per via grafica i parametri di tale andamento
e associarli, attraverso le (2.1-2.2)
alle grandezze fisiche di interesse (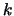 e
e 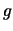 ).
).
Definiamo la procedura in via generale pensando a due quantità
 e
e 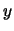 legate dalla relazione
legate dalla relazione
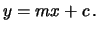 |
(6.3) |
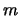 e
e 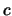 sono rispettivamente il coefficiente angolare
(o pendenza, in inglese ``slope'')
e l'intercetta della retta. Per analizzare i dati
ci si basa sul seguente modello:
sono rispettivamente il coefficiente angolare
(o pendenza, in inglese ``slope'')
e l'intercetta della retta. Per analizzare i dati
ci si basa sul seguente modello:
- l'equazione (6.3) è quella ipotizzata
dai valori veri delle grandezze fisiche.
- i punti sperimentali non giacciono tutti sulla retta - nel
senso geometrico - a causa degli inevitabili errori di misura;
- la migliore stima della retta vera è quella che
passa meglio per i punti. Per ora la sua valutazione
sarà effettuata ad occhio cercando, mediante
un righello trasparente, di trovare la retta che meglio
approssima globalmente i punti.
Trovata la retta che meglio si adatta ai dati
i parametri 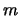 e
e 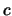 sono determinati
considerando due punti,
in principio
``arbitrari'',
appartenenti
alla retta. Chiamando i due punti
sono determinati
considerando due punti,
in principio
``arbitrari'',
appartenenti
alla retta. Chiamando i due punti
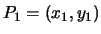 e
e
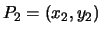 si può scrivere
l'equazione parametrica della
retta
si può scrivere
l'equazione parametrica della
retta
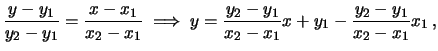 |
(6.4) |
ovvero
È da notare che, mentre la (6.5) è effettivamente usata per
la stima di 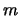 , per valutare l'intercetta si preferisce
determinare direttamente,
per via grafica, il valore per il
quale la retta interseca l'asse delle ordinate
(a meno che lo zero dell'asse delle ascisse
sia fuori scala):
, per valutare l'intercetta si preferisce
determinare direttamente,
per via grafica, il valore per il
quale la retta interseca l'asse delle ordinate
(a meno che lo zero dell'asse delle ascisse
sia fuori scala):
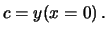 |
(6.7) |
Per quanto riguarda la scelta dei punti per valutare 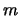 (ed eventualmente
(ed eventualmente
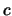 ) si seguono questi criteri:
) si seguono questi criteri:
- i punti vanno scelti sulla retta e non in corrispondenza dei valori
sperimentali (a meno che per un puro caso un punto sperimentale
non giaccia esattamente sulla retta). Infatti, nonostante intuitivamente
si possa pensare che un punto misurato sia ``più vero'' di un generico
punto sulla retta, i punti della retta tengono conto simultanemente
di tutti i punti misurati e quindi sono meno sensibili alle possibili
fluttuazioni legate all'errore della singola misura;
- i punti vanno scelti in modo che siano ben leggibili e quindi
preferibilmente in prossimità dell'incrocio di due linee della carta
millimetrata;
- al fine di ridurre l'incertezza dovuta alla lettura
dei punti
è opportuno scegliere questi
molto lontani fra di loro. Infatti, facendo riferimento
alla (6.5), ci si può facilmente convincere
che il numero di cifre significative su
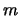 ottenibili
con il metodo grafico è legata al numero di cifre
significative del numeratore e del denominatore. Queste
ultime dipendono a loro volta dal valore assoluto
di
ottenibili
con il metodo grafico è legata al numero di cifre
significative del numeratore e del denominatore. Queste
ultime dipendono a loro volta dal valore assoluto
di 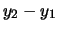 e di
e di 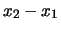 (si provi a considerare
il limite di due punti molto vicini);
(si provi a considerare
il limite di due punti molto vicini);




Next: Cifre significative dei parametri
Up: Analisi grafiche
Previous: Grafici
Indice
Giulio D'Agostini
2001-04-02


![]() e
e ![]() ).
).
![]() e
e ![]() legate dalla relazione
legate dalla relazione
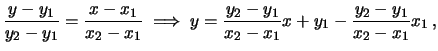
![]() (ed eventualmente
(ed eventualmente
![]() ) si seguono questi criteri:
) si seguono questi criteri: