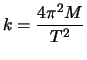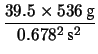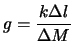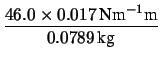Next: pzd100 Potere di aspirazione
Up: Allungamento e periodo di
Previous: Misure
Indice
Cerchiamo di valutare 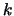 e
e 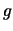 dalla differenza di allungamento
dovuta all'aggiunta del
sesto dischetto. Prendendo i dati della
prima serie di misure, dalla (2.2) si ottiene2.2
dalla differenza di allungamento
dovuta all'aggiunta del
sesto dischetto. Prendendo i dati della
prima serie di misure, dalla (2.2) si ottiene2.2
Poiché l'allungamento della molla causato dall'aggiunta del sesto dischetto
(
 g)
è stato di
g)
è stato di
 mm = 0.017 m si ottiene
mm = 0.017 m si ottiene
È da notare come il valore di 9.9 m/s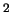 potrebbe indurre a credere
che
potrebbe indurre a credere
che 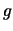 sia stata determinata
con un incertezza di qualche parte per cento. In realtà
ai fini dell'esatta valutazione di
sia stata determinata
con un incertezza di qualche parte per cento. In realtà
ai fini dell'esatta valutazione di
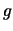 è determinante il contributo di
è determinante il contributo di
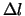 . Infatti non ci sarebbe da meravigliarsi se esso venisse
in altre misure 0.016 o 0.018cm, o anche se deviasse un po' di più
da 0.017cm. Quindi
. Infatti non ci sarebbe da meravigliarsi se esso venisse
in altre misure 0.016 o 0.018cm, o anche se deviasse un po' di più
da 0.017cm. Quindi 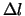 è determinato a circa
1 parte su 17, ovvero al 6%.
Questo si rifletterebbe su
è determinato a circa
1 parte su 17, ovvero al 6%.
Questo si rifletterebbe su 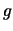 con una incertezza
dell'ordine
di 0.6 m/s
con una incertezza
dell'ordine
di 0.6 m/s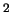 . Pertanto l'ottimo accordo con il ``valore vero''
di 9.8 m/s
. Pertanto l'ottimo accordo con il ``valore vero''
di 9.8 m/s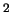 è da ritenersi soltanto un caso fortunato.
è da ritenersi soltanto un caso fortunato.
Possiamo ripetere lo stesso esercizio per le tre serie
e, considerando anche le variazioni dal sesto al settimo
e dal settimo all'ottavo dischetto,
riportare i risultati in tabella 2.6.
Tabella:
Valori della costante elastica della molla (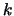 )
e dell'accelerazione di gravità ottenuti da un'analisi
parziale della tabella 2.5.
)
e dell'accelerazione di gravità ottenuti da un'analisi
parziale della tabella 2.5.
|
|
Prima serie |
Seconda serie |
Terza serie |
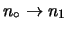
|
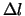 |
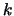 |
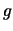
|
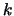 |
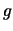
|
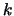 |
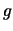 |
|
|
(mm) |
(N/m) |
(m/s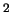 ) ) |
(N/m) |
(m/s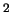 ) ) |
(N/m) |
(m/s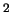 ) ) |
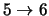 |
17 |
46.0 |
9.9 |
45.5 |
9.8 |
43.9 |
9.5 |
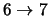 |
19 |
45.8 |
11.0 |
45.2 |
10.9 |
45.2 |
10.9 |
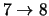 |
18 |
45.1 |
10.3 |
44.9 |
10.3 |
44.3 |
10.1 |
|
I risultati mostrano valori di 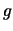 confrontabili con
il valore atteso di 9.80 m/s
confrontabili con
il valore atteso di 9.80 m/s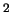 . La differenza fra ciascuno
dei valori misurati e il valore ``vero'' di
. La differenza fra ciascuno
dei valori misurati e il valore ``vero'' di 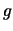 ci dà un'idea
dell'errore commesso nella misura. Esso varia fra
ci dà un'idea
dell'errore commesso nella misura. Esso varia fra
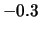 e
e 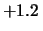 m/s
m/s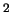 . Abbiamo ottenuto variazioni
comprese fra
. Abbiamo ottenuto variazioni
comprese fra 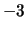 e
e 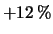 rispetto al valore vero,
ovvero errori percentuali (in valore assoluto)
dell'ordine del
rispetto al valore vero,
ovvero errori percentuali (in valore assoluto)
dell'ordine del 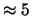 -10%.
-10%.
Purtroppo non è usuale nella ricerca
sapere già
il risultato della misura,
in quanto non è interessante
perdere tempo a misurare una grandezza nota con esattezza,
se non per ragioni didattiche o per
per calibrare
l'apparato sperimentale e il metodo di misura.
In genere prima della misura
il risultato di interesse è sempre ignoto o
incerto (si crede che sia più in un certo intervallo che altrove).
È quindi
importante essere in grado di
stimare l'ordine di grandezza
dell'errore (ignoto!) che può essere stato commesso
senza conoscere il
valore vero della grandezza da misurare. Questo è uno degli scopi
di questo corso e l'argomento verrà trattato ampiamente nel seguito.
Dai dati di tabella 2.5 e dai risultati ottenuti
in tabella 2.6 sorgono spontanee alcune domande
- I risultati sono stati ottenuti dall'ipotesi di linearità dell'allungamento
dalla massa applicata e dalla formula 2.2.
La relativa stabilità dei valori ottenuti e l'accordo qualitativo
con il valore vero di
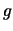 indicano che tali ipotesi
sono ragionevoli. È possibile stabilire dei criteri per verificare
tali ipotesi? È possibile analizzare soltanto
i dati che meglio soddisfano tali ipotesi al fine di diminuire
gli errori?
indicano che tali ipotesi
sono ragionevoli. È possibile stabilire dei criteri per verificare
tali ipotesi? È possibile analizzare soltanto
i dati che meglio soddisfano tali ipotesi al fine di diminuire
gli errori?
- Come si possono combinare insieme tutte le informazioni di una
serie di misure per ottenere un valore di
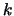 e di
e di 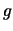 ?
Si sarebbe tentati di mediare in qualche modo
i valori
di
?
Si sarebbe tentati di mediare in qualche modo
i valori
di 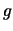 ottenuti. Bisogna però prestare attenzione al fatto
che,
con il metodo utilizzato sopra, ogni misura di allungamento
influenza due valori di
ottenuti. Bisogna però prestare attenzione al fatto
che,
con il metodo utilizzato sopra, ogni misura di allungamento
influenza due valori di 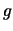 . Per esempio, se al posto di
. Per esempio, se al posto di
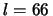 mm per
mm per  si fosse misurato
si fosse misurato 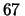 mm
(non improbabile) i due valori di
mm
(non improbabile) i due valori di 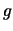 corrispondenti
della tabella 2.6 sarebbero diventati
rispettivamente
corrispondenti
della tabella 2.6 sarebbero diventati
rispettivamente 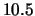 e
e 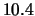 m/s
m/s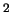 .
.
Come al solito, prima di poter dare una risposta a tale domande
occorrerà aver acquisito delle conoscenze teoriche di probabilità
e di statistica.




Next: pzd100 Potere di aspirazione
Up: Allungamento e periodo di
Previous: Misure
Indice
Giulio D'Agostini
2001-04-02