



Next: Continua ...
Up: Primo sguardo ai dati
Previous: Prime valutazioni di e
Indice
Questa esperienza è molto istruttiva
ai fini dell'apprendimento dell'analisi
dei dati. Viene introdotta in questo capitolo
e l'analisi grafica viene lasciata come esercizio sulle
linearizzazioni. Successivamente verrà ripresa in dettaglio
quando si parlerà dei fit.
Consideriamo una pompa da vuoto connessa ad un recipiente
e messa in funzione a partire da un istante  . Essa produrrà
una depressione nella linea del vuoto (definita come l'insieme
della pompa,
recipienti, tubi, raccordi, rubinetti e manometro opportunamente
connessi fra di loro).
Dall'istante in cui il circuito è chiuso a tenuta
l'andamento della depressione
. Essa produrrà
una depressione nella linea del vuoto (definita come l'insieme
della pompa,
recipienti, tubi, raccordi, rubinetti e manometro opportunamente
connessi fra di loro).
Dall'istante in cui il circuito è chiuso a tenuta
l'andamento della depressione 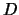 in funzione del tempo è di tipo
esponenziale
in funzione del tempo è di tipo
esponenziale
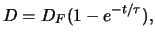 |
(2.5) |
caratterizzato da una costante di tempo 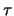 che dipende dal volume totale della linea di vuoto e dalla
potenza della pompa, quantificata nella cosiddetta
velocità di aspirazione, definita
da
che dipende dal volume totale della linea di vuoto e dalla
potenza della pompa, quantificata nella cosiddetta
velocità di aspirazione, definita
da
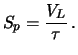 |
(2.6) |
È possibile ottenere 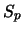 dalla misura della costante di tempo
per un dato valore di
dalla misura della costante di tempo
per un dato valore di 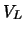 . Ma il volume totale della linea
contiene un contributo costante - ma di difficile misura -
dovuto alla pompa stessa, raccordi e manometro, che indicheremo
con
. Ma il volume totale della linea
contiene un contributo costante - ma di difficile misura -
dovuto alla pompa stessa, raccordi e manometro, che indicheremo
con 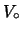 . È quindi
opportuno effettuare misure di
. È quindi
opportuno effettuare misure di 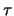 per diversi volumi
per diversi volumi
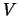 del recipiente e dalla relazione
del recipiente e dalla relazione
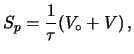 |
(2.7) |
ovvero
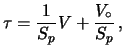 |
(2.8) |
ottenere 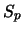 e
e 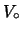 .
.
Ai fini delle misure, effettuate con un normale manometro, e dell'analisi
è preferibile esprimere
la (2.5) come:
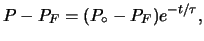 |
(2.9) |
o
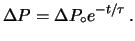 |
(2.10) |
dove 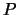 è la pressione misurata all'istante
è la pressione misurata all'istante 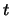 ,
, 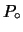 è la
pressione all'istante
è la
pressione all'istante  e
e 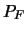 è la pressione
raggiunta asintoticamente.
è la pressione
raggiunta asintoticamente.
I dati sperimentali degli andamenti di 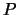 in funzione di
in funzione di 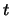 per
tre volumi sono riportati in tabella 2.7.
Essi sono dati reali
raccolti da un gruppo di studenti.
per
tre volumi sono riportati in tabella 2.7.
Essi sono dati reali
raccolti da un gruppo di studenti.
Tabella:
Dati sperimentali dell'andamento della pressione
all'interno di una linea da vuoto in funzione del tempo e del volume
del recipiente 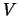 . Il volume totale della linea contiene anche un
contributo costante
. Il volume totale della linea contiene anche un
contributo costante 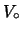 dovuto alla pompa stessa e ai raccordi.
Per semplicità le misure dirette di
dovuto alla pompa stessa e ai raccordi.
Per semplicità le misure dirette di 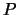 e
e 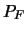 sono
presentate come differenza
sono
presentate come differenza
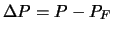 . Si noti come nelle
misure per
. Si noti come nelle
misure per 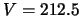 ml
non è stata eseguita la lettura
del decimo e quindi tale informazione
non è recuperabile. Ciò
può essere dovuto al fatto che queste misure
sono state effettuate per prime e soltanto successivamente gli studenti
hanno deciso di poter apprezzare i decimi. Sarà interessante
vedere al momento opportuno, mediante l'analisi dei residui, se
i decimi sono significativi.
ml
non è stata eseguita la lettura
del decimo e quindi tale informazione
non è recuperabile. Ciò
può essere dovuto al fatto che queste misure
sono state effettuate per prime e soltanto successivamente gli studenti
hanno deciso di poter apprezzare i decimi. Sarà interessante
vedere al momento opportuno, mediante l'analisi dei residui, se
i decimi sono significativi.
| |
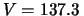 ml ml |
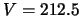 ml ml |
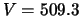 ml ml |
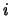 |
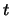 |
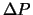 |
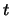 |
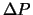 |
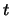 |
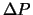 |
| |
(s) |
(cmHg) |
(s) |
(cmHg) |
(s) |
(cmHg) |
| 1 |
2.0 |
45.0 |
4.0 |
45 |
6.0 |
50.8 |
| 2 |
4.0 |
34.5 |
8.0 |
31 |
12.0 |
39.3 |
| 3 |
6.0 |
26.5 |
12.0 |
22 |
18.0 |
31.8 |
| 4 |
8.0 |
22.5 |
16.0 |
16 |
24.0 |
25.3 |
| 5 |
10.0 |
17.0 |
20.0 |
13 |
30.0 |
20.8 |
|




Next: Continua ...
Up: Primo sguardo ai dati
Previous: Prime valutazioni di e
Indice
Giulio D'Agostini
2001-04-02
![]() . Essa produrrà
una depressione nella linea del vuoto (definita come l'insieme
della pompa,
recipienti, tubi, raccordi, rubinetti e manometro opportunamente
connessi fra di loro).
Dall'istante in cui il circuito è chiuso a tenuta
l'andamento della depressione
. Essa produrrà
una depressione nella linea del vuoto (definita come l'insieme
della pompa,
recipienti, tubi, raccordi, rubinetti e manometro opportunamente
connessi fra di loro).
Dall'istante in cui il circuito è chiuso a tenuta
l'andamento della depressione ![]() in funzione del tempo è di tipo
esponenziale
in funzione del tempo è di tipo
esponenziale
![]() in funzione di
in funzione di ![]() per
tre volumi sono riportati in tabella 2.7.
Essi sono dati reali
raccolti da un gruppo di studenti.
per
tre volumi sono riportati in tabella 2.7.
Essi sono dati reali
raccolti da un gruppo di studenti.