Next: pzd100Simulazioni
Up: Previsioni dei risultati
Previous: Ginnastica riepilogativa
Indice
Nei paragrafi precedenti abbiamo confrontato più volte
le previsioni delle distribuzioni statistiche
con quanto ottenuto
nelle esperienze simulate e, praticamente, ogni volta
queste ultime erano in ottimo accordo con le aspettative
(tenendo conto delle incertezze di previsione). Al fine
di togliere di mente a qualcuno che si fosse fatto
l'idea strana che ``la distribuzione sperimentale
si è verificata perché era altamente probabile'',
calcoliamo ora la probabilità di una particolare
distribuzione. Per semplicità, consideriamo nuovamente
l'esperienza del contatore, ed, in particolare, l'esperimento
del numero di conteggio a tempi prefissati. Cominciamo con il caso di
 s. Le probabilità sono già state
riportate nella tabella 7.3. Le previsioni della
frequenza dei
possibili numeri di conteggi osservabili in 100
misure sono:
s. Le probabilità sono già state
riportate nella tabella 7.3. Le previsioni della
frequenza dei
possibili numeri di conteggi osservabili in 100
misure sono:
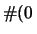 conteggi conteggi |
 |
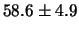 |
|
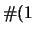 conteggi conteggi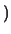 |
 |
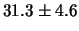 |
|
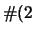 conteggi conteggi |
 |
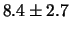 |
|
 conteggi conteggi |
 |
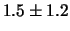 |
|
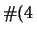 conteggi conteggi |
 |
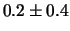 |
|
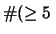 conteggi conteggi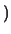 |
 |
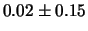 |
|
La distribuzione osservata, con una frequenza di conteggi
da 0 a 4 rispettivamente di 56, 32, 9, 2 e 1 occorrenze,
è in ottimo accordo con le previsioni. Ciò nonostante
la probabilità di osservare tale risultato (ovviamente
``prima'' dell'esperimento, o comunque non conoscendone
l'esito), è molto piccola, come calcolabile facendo
uso della distribuzione multinomiale7.3
e delle probabilità
della tabella 7.3:
Per confronto, riportiamo nella tabella 7.6
altre distribuzioni che sarebbero ugualmente risultate in
``buon accordo''
con le previsioni (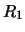 -
-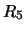 ), altre per le quali l'accordo sarebbe
stato giudicato ``marginale'' (
), altre per le quali l'accordo sarebbe
stato giudicato ``marginale'' (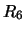 -
-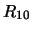 ) e altre
che sarebbero risultate ``sospette''
(
) e altre
che sarebbero risultate ``sospette''
(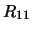 -
-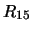 ).
).
Tabella:
Possibili risultati di 100 misure
di conteggio da 3 secondi relative ad
un fenomeno descritto da un processo di Poisson
di intensità 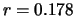 conteggi al secondo.
conteggi al secondo.
| Risultati |
Numero di conteggi |
Probabilità |
| |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
| |
|
|
|
|
|
|
|
|
|
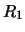 |
56 |
32 |
9 |
2 |
1 |
0 |
0 |
0 |
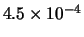 |
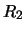 |
63 |
29 |
7 |
3 |
0 |
0 |
0 |
0 |
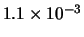 |
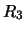 |
59 |
31 |
8 |
2 |
0 |
0 |
0 |
0 |
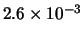 |
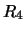 |
54 |
36 |
7 |
2 |
1 |
0 |
0 |
0 |
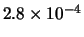 |
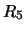 |
55 |
34 |
10 |
1 |
0 |
0 |
0 |
0 |
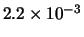 |
| |
|
|
|
|
|
|
|
|
|
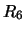 |
52 |
37 |
8 |
3 |
0 |
0 |
0 |
0 |
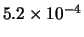 |
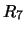 |
70 |
22 |
5 |
2 |
1 |
0 |
0 |
0 |
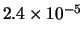 |
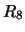 |
69 |
26 |
4 |
0 |
1 |
0 |
0 |
0 |
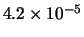 |
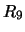 |
53 |
29 |
13 |
3 |
1 |
1 |
0 |
0 |
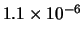 |
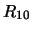 |
52 |
27 |
15 |
5 |
0 |
1 |
0 |
0 |
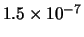 |
| |
|
|
|
|
|
|
|
|
|
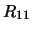 |
45 |
28 |
18 |
5 |
3 |
1 |
0 |
0 |
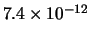 |
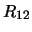 |
71 |
19 |
2 |
1 |
3 |
1 |
2 |
1 |
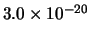 |
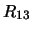 |
90 |
5 |
2 |
1 |
0 |
1 |
0 |
1 |
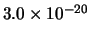 |
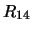 |
24 |
52 |
0 |
8 |
0 |
4 |
4 |
8 |
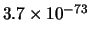 |
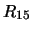 |
0 |
100 |
0 |
0 |
0 |
0 |
0 |
0 |
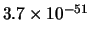 |
|
Si noti comunque che nessuna
delle distribuzioni è incompatibile con le previsioni.
Questo dovrebbe servire ad abituarsi all'idea che
una legge probabilistica non può mai essere falsificata.
Al più, si potrà attribuire ad essa un basso grado di fiducia
alla luce dei dati osservati e della possibilità di altre ipotesi.
Si noti inoltre come la probabilità di una
possibile distribuzione dipende da quanti sono i possibili
esiti che hanno probabilità confrontabile fra loro e
per i quali ci si attende una frequenza di conteggio sostanzialmente
diversa da zero. Ad esempio le misure di conteggio
a 100 secondi (tabella 4.1)
mostrano un buon accordo con le previsioni
(tabella 7.3), ma la loro probabilità
sarebbe stata
Finora abbiamo considerato soltanto la probabilità
di distribuzioni statistiche, ovvero avendo
già raggruppato
i possibili esiti sotto forma di tabella e avendo
considerato la frequenza con la quale ciascun
esito si può verificare. Non si è tenuto
conto dell'ordine con cui si possono presentare
i possibili esiti. Nel caso dei dati del contatore
per  s la probabilità di osservare una sequenza
come quella della tabella 1.1
vale:
s la probabilità di osservare una sequenza
come quella della tabella 1.1
vale:
Il motivo per cui la probabilità della distribuzione
è invece 42 ordini di grandezze maggiore è dovuto
al grandissimo numero di sequenze che possono
produrre la stessa distribuzione, dato dal coefficiente
multinomiale
Ovviamente, nel caso delle misure da 100 secondi
la probabilità della particolare sequenza sarà
ancora più piccola, ed esattamente
e, ciò nonostante, ...l'abbiamo osservata.
Si faccia quindi attenzione ad espressioni fuorvianti del
tipo ``praticamente impossibile'' riferito ad eventi
che riteniamo molto poco probabili (ad esempio
aventi probabilità inferiore a 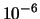 ). È vero sì che essi
possono avere probabilità ``praticamente nulla'',
ma non è corretto escludere tali eventi dalle nostre considerazioni,
altrimenti può accadere, come nell'esempio che stiamo trattando,
di dover escludere tutti i possibili esiti dell'esperimento.
). È vero sì che essi
possono avere probabilità ``praticamente nulla'',
ma non è corretto escludere tali eventi dalle nostre considerazioni,
altrimenti può accadere, come nell'esempio che stiamo trattando,
di dover escludere tutti i possibili esiti dell'esperimento.




Next: pzd100Simulazioni
Up: Previsioni dei risultati
Previous: Ginnastica riepilogativa
Indice
Giulio D'Agostini
2001-04-02
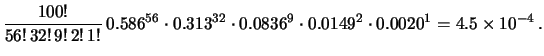
![]() s la probabilità di osservare una sequenza
come quella della tabella 1.1
vale:
s la probabilità di osservare una sequenza
come quella della tabella 1.1
vale: