Next: pzd100Le distribuzioni osservate ``erano''
Up: Previsioni dei risultati
Previous: Cammino casuale (random walk)
Indice
Già nelle applicazioni precedenti abbiamo cercato di
mostrare come si passi da una distribuzione
all'altra nell'ambito di uno stesso problema.
Non ci si deve abituare a pensare ``problema della binomiale'',
al ``problema dell poissoniana'' e così via,
come fanno i bambini quando chiedono
se il problema è ``quello del più''
o ``quello del per''.
Facciamo un esempio, che può risultare artificioso, ma che
sicuramente dovrebbe servire alla scopo.
Consideriamo 23 classi di 30 studenti ciascuna. Ogni studente
esegue l'esperienza del pallinometro a 32 file di chiodi
e, nell'ambito di ogni classe si calcola la media del numero di palline
che cade nel bin 10.
Quanto vale la probabilità che almeno 2 delle 23 medie
sia maggiore di 153? Quanto vale la probabilità di avere
esattamente 3 medie che soddisfano tale condizione?
Risolviamo il problema in modo schematico, lasciando
i conti per esercizio:
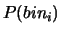 |
 |
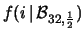 |
|
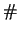 palline palline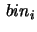 |
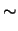 |
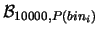 |
|
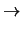 |
 |
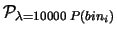 |
|
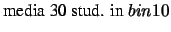 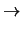 |
 |
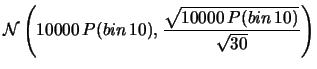 |
|
 media media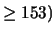 |
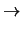 |
vedi tabelle distr. normale |
|
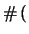 media media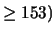 |
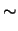 |
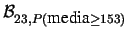 |
|
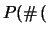 media media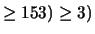 |
 |
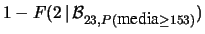 |
|
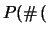 media media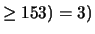 |
 |
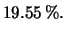 |
|
Nel penultimo passaggio 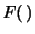 indicava la distribuzione
cumulativa. Il risultato finale è dato per
permettere di verificare i conti.
indicava la distribuzione
cumulativa. Il risultato finale è dato per
permettere di verificare i conti.




Next: pzd100Le distribuzioni osservate ``erano''
Up: Previsioni dei risultati
Previous: Cammino casuale (random walk)
Indice
Giulio D'Agostini
2001-04-02