${\bf\circlearrowright\,}$ Cammino casuale (random walk)

È interessante reinterpratare l'esperienza del pallinometro, pensando che la distanza fra le file di chiodi rappresenti il tempo che intercorre fra un'osservazione e l'altra.

Figura: Processo di Bernoulli nel dominio del tempo.

La figura 7.1, ottenuta ruotando la figura 1.2, e interpretando la distanza fra le file di chiodi come il tempo (quantizzato) che intercorre fra istanti di possibili osservazioni successivi, rappresenta movimento a caso su una dimensionale di un punto materiale in funzione del tempo. Ad ogni intervallino di tempo il punto avanza o indietra ``a caso'' (con probabilità 1/2). Questo cammino casuale schematizza molti processi aleatori, come il moto browniano unidimensionale o la situazione finanziare di un giocatore d'azzardo (la posizione rappresenta il guadagnmo netto dopo $n$ scommesse).

• Per quanto riguarda il moto browniano, si ricorda come Einstein aveva trovato una soluzione gaussiana con deviazione standard proporzionale alla radice quadrata del tempo (corrispondente a 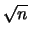$\sqrt{n}$ nella nostra schematizzazione).
• Una interessante applicazione ai giochi d'azzardo riguarda la soluzione del problema della ``rovina del giocatore''. Si tratta di valutare la probabilità che, nel corso del gioco, si raggiunga alla massima perdita sostenibile, corrispondente al capitale massimo a disposizione del giocatore.
• Infine, il cammino casuale aiuta a modellizzare il rumore introdotto in una catena di misura e che fa deviare il segnale di misura dal caso ideale (vedi schema della figura 8.2). Questo cammino casuale in uno spazio astratto giustifica la distribuzione gaussiana degli errori di misura.