



Next: osservazioni indipendenti con nota
Up: Misure dirette con verosimiglianza
Previous: Condizioni di ripetitibità
Indice
Si osserva  . Siccome si crede che i possibili valori dell'osservabile
abbiano una distribuzione di probabilità gaussiana con
intorno a
. Siccome si crede che i possibili valori dell'osservabile
abbiano una distribuzione di probabilità gaussiana con
intorno a 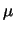 , dall'inversione di probabilità
si ha che i possibili valori di
, dall'inversione di probabilità
si ha che i possibili valori di 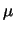 hanno una analoga distribuzione
di probabilità intorno a
hanno una analoga distribuzione
di probabilità intorno a  con
Espresso in modo sintetico:
con
Espresso in modo sintetico:
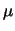 prior uniforme prior uniforme![$\displaystyle ]{}\mu\sim {\cal N}(x, \sigma_R)$](img1315.png) |
(10.1) |
Ne segue che
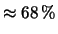 |
 |
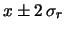 al al 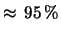 di probabilità di probabilità |
|
| |
 |
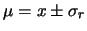 al al 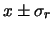 di probabilità di probabilità |
|
| |
 |
... |
|
Nel seguito considereremo come standard l'incertezza data ad una deviazione
standard, essa è chiamata
incertezza standard (vedi paragrafo 11.7).
Concludiamo questo paragrafo invitando a riflettere al significato
probabilistico di espressioni del tipo
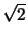 sul quale è già stato detto precedentemente e a diffitare
da interpretazioni del tipo ``se io ripetessi la misura
un grande numero di volte, allora nel 68,3% dei casi
otterrei risultati compresi nell'intervallo
sul quale è già stato detto precedentemente e a diffitare
da interpretazioni del tipo ``se io ripetessi la misura
un grande numero di volte, allora nel 68,3% dei casi
otterrei risultati compresi nell'intervallo
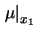 '': oltre a
forzature interpretative si commette un errore numerico di
'': oltre a
forzature interpretative si commette un errore numerico di 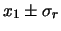 :
come mai?
:
come mai?




Next: osservazioni indipendenti con nota
Up: Misure dirette con verosimiglianza
Previous: Condizioni di ripetitibità
Indice
Giulio D'Agostini
2001-04-02
![]() sul quale è già stato detto precedentemente e a diffitare
da interpretazioni del tipo ``se io ripetessi la misura
un grande numero di volte, allora nel 68,3% dei casi
otterrei risultati compresi nell'intervallo
sul quale è già stato detto precedentemente e a diffitare
da interpretazioni del tipo ``se io ripetessi la misura
un grande numero di volte, allora nel 68,3% dei casi
otterrei risultati compresi nell'intervallo
![]() '': oltre a
forzature interpretative si commette un errore numerico di
'': oltre a
forzature interpretative si commette un errore numerico di ![]() :
come mai?
:
come mai?