



Next: Analisi grafiche
Up: Descrizione quantitativa dei dati
Previous: Nota sulle cifre significative
Indice
- Dimostrare che la media degli scarti è nulla.
- Valutare moda, mediana e media e deviazione standard
dei seguenti dati statistici:
6, 7, 10, 1, 8, 12, 7, 5, 7, 9, 6, 8.
- Valutare moda, mediana e media e deviazione standard
dei seguenti dati statistici:
0, 6, 7, 10, 1, 8, 0, 12, 7, 5, 7, 9, 6, 8.
- Valutare moda, mediana e media e deviazione standard
dei seguenti dati statistici:
3, 4, 0, 6, 7, 10, 1, 8, 0, 12, 7, 5, 7, 9, 6, 8.
- Valutare moda, mediana e media e deviazione standard
dei seguenti dati statistici:
6, 3, 4, 0, 6, 7, 10, 1, 8, 0, 12, 7, 5, 7, 9, 6, 8.
- Calcolare moda, mediana,
media, deviazione standard e coefficiente di variazione
delle distribuzioni
di conteggi per 6, 12 e 30 della
tabella 4.1, riportando anche i valori di
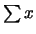 e di
e di
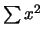 .
.
- Trovare moda, mediana, media, deviazione standard
e coefficiente di variazione della distribuzione
di conteggi per 100 secondi della tabella 4.2.
- Trovare moda, mediana, media, deviazione standard
e coefficiente di variazione della distribuzione
di conteggi per 300 secondi della tabella 4.2.
- Calcolare media e deviazione standard dei seguenti valori:
1000000.2, 1000000.3, 1000000.1, 1000000.2, 1000000.4
- Calcolare media e deviazione standard degli scarti fra i valori stimati e
quelli letti al nonio dello studente L.T. della tabella
2.2.
Se quantifichiamo l'errore tipico con la
deviazione standard degli scarti e in una misura successiva
effettuata nelle stesse condizioni egli affermerà
di leggere 44.76 cm quanto si crederà a tale valore?
- Da 100 valori si ottiene
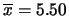 e
e
 .
Altri 50 valori danno
.
Altri 50 valori danno
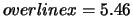 e
e
 . Quanto
valgono media e deviazione standard raggruppando i 150 valori?
. Quanto
valgono media e deviazione standard raggruppando i 150 valori?




Next: Analisi grafiche
Up: Descrizione quantitativa dei dati
Previous: Nota sulle cifre significative
Indice
Giulio D'Agostini
2001-04-02