Fisica per il CdS in SMIA

Prof. G. D'Agostini

A.A. 23-24

Problemi proposti per ciascuna lezione

     -------------           -------------        1. Gio 29/02  
  2. Lun 4/03     3. Mar 5/03     4. Gio 7/03  
  5. Lun 11/03     6. Mar 12/03     7. Gio 14/03  
  8. Lun 18/03     9. Mar 19/03     10. Gio 21/03  
  11. Lun 25/03     12. Mar 26/03   -------------
     -------------           -------------        13. Gio 4/04  
  14. Lun 8/04     15. Mar 9/04     16. Gio 11/04  
  17. Lun 15/04     18. Mar 16/04     19. Gio 18/04  
  20. Lun 22/04     21. Mar 23/04   -------------
  22. Lun 29/04     23. Mar 30/04     24. Gio 2/05  
  25. Lun 6/05     26. Mar 7/05     27. Gio 9/05  
  28. Lun 13/05     29. Mar 14/05     30. Gio 16/05  
  31. Lun 20/05     32. Mar 21/05     33. Gio 23/05  
  34. Lun 27/05      ------------      35. Gio 30/05  
36. Lun 3/06      -------------           -------------     
Lezione 1 (29/02, 2h)
 
Problemi proposti
  1. Vedere sul file pdf
 
Torna su   —   Galleria   —   Home  
Lezione 2 (4/03, 3h)
 
Problemi proposti
  1. Quesito nr. 19
    • arrivando prima alla 'formula risolutrice' (senza valori numerici),
    • sostituendo successivamente i valori numerici
    • e trattando algebricamente le unità di misura (che non vanno 'inventate' sapendo cosa ci si aspetta).
  2. Variante nel quesito precedente, con n intervalli temporali Δti,
    ciascuno percorso con velocità vi (solo formula risolutrice).
    Come si interpreta la formula che si ottiene?
  3. Problema di una velocità (lungo x) che varia nel tempo secondo un esponenziale decrescente,
    ovvero vx(t) = vx0e-t/τ, con
    • vx0 = vx(t=0) = 100 km/h;
    • τ = 1' (ovvero 60s).
    1. Calcolare il valore della velocità per t=0, t=τ, t=2τ e t=5τ, t=10τ.
    2. Valutare l'espressione dell'accelerazione in funzione del tempo, ovvero ax(t).
    3. Calcolare il valore dell'accelerazione (con il segno corretto!) per t=0, t=τ, t=2τ, t=5τ e t=10τ.
    4. Calcolare l'espressione dello spazio percorso da t=0 al generico t, ovvero di x(t), avendo posto x(t=0)=0.
    5. Calcolare l'espressione di x(t) per t=τ, t=2τ, t=5τ e t → ∞.
  4. Plottare con il programma di grafica preferito vx(t), ax(t) e x(t) da t=0 a t=5τ.
 
Torna su   —   Galleria   —   Home  
Lezione 3 (5/03, 2h)
 
Problemi proposti
  1. Risolvere il problema della distanza da cui è stato fotografato il Cupolone (→ Galleria)
     
  2. Supponendo che ad un certo istante (t=0) un oggetto
    • si trovi in (x0, y0)
    • abbia una velocità iniziale (vx0, vy0)
    • e per t≥0 sia abbia una accelerazione costante (ax, ay),
    ricavarsi (*)
    1. l'espressione delle componenti della velocità al generico t≥0;
    2. le equazioni orarie x(t) e y(t).
    [(*) Nota: gli integrali di interesse andranno da 0 a t e quindi la variabile di integrazione andrà indicata con t'.]
     
  3. Caso particolare della soluzione del problema precedente:
    • moto unidimensionale verticale, a cui associeremo l'asse cartesiano x, diretto per comodità verso il basso;
    • condizioni iniziali: x0=0 e vx0=0;
    • accelerazione costante ax=g (la ben nota 'g').
    1. Ricavarsi le espressioni di
      • vx(t);
      • x(t).
    2. Usando il valore numerico g=9.8 m/s2 ricavarsi
      • la velocità a t=1s, t=2s e t=3s;
      • la posizione a t=1s, t=2s e t=3s.

  4. Altro caso particolare:
    • moto bidimensionale, con l'asse x disposto orizzontalmente e l'asse y verticalmente e diretto verso l'alto;
    • posizione iniziale nell'origine: x0=0 e y0=0;
    • velocità iniziali vx0 e vy0;
    • accelerazione costante con ax=0 e ay=-g.
    1. Riscrivere le espressioni generali di velocità e posizione, ricavate precedentemente, per questo caso particolare.
    2. Ricavarsi le espressioni del tempo t che soddisfano alle seguenti condizioni:
      1. v(t)=0   (indicare questo tempo con il simbolo tM);
      2. y(t)=0   (indicare la soluzione 'non banale' con tG).
    3. Ricavarsi le espressioni di x(t=tM) e x(t=tG).
    4. Calcolarsi le soluzioni numeriche dei quesiti 2 e 3 per vx0=vy0=10m/s.
     
  5. Dalle espressioni di x(t) e di y(t) ricavate nel problema precedente (punto 1.),
    ↠ trovare l'equazione della traiettoria, ovvero y(x).
     
  6. Un escursionista tende il braccio in una certa direzione, tenendo il pollice verticale.
    Così facendo, il pollice copre esattamente un'auto in lontananza, posta trasversalmente alla direzione di vista.
    Sapendo che la larghezza del pollice è di 2.2 cm, la sua distanza dall'occhio è di 59 cm
    e che la lunghezza dell'auto è di 4 m, si valuti a che distanza dall'escursionista si trova l'auto.
 
Torna su   —   Galleria   —   Home  
Lezione 4 (7/03, 2h)
 
Problemi proposti
  1. Velocità e accelerazione di un punto materiale avente x(t) e y(t) dati sopra.
  2. Ricavarsi la formula del volume di una sfera sommando infinti dischetti di spessore infinitesimo.
  3. Misurare la densità degli oggetti di cui abbiamo effettuato misure in aula.
  4. Ancora sul problema nr. 1, ricordando che per definizione un 'versore' è pari al vettore diviso il suo modulo
    (e quindi un versore ha modulo unitario e fornisce solo direzione e verso):
    1. valutarsi i versori dei tre vettori del problema;
    2. disegnare su un grafico cartesiano i tre versori per
      • t = 0 e t = π/(2ω)
      → come sono orientati, l'uno rispetto all'altro, i tre versori?
      → cosa ci aspettiamo che avvenga quindi al generico tempo t?
 
Torna su   —   Galleria   —   Home  
Lezione 5 (11/03, 3h)
 
Problemi proposti
  1. Valutare la densità della sfera di piombo con le misure effettuate a lezione.
  2. Valutare la densità del blocco di polistirolo trascurando la spinta di Archimede dell'aria.
  3. Dalla densità dell'aria 'tipica' (→ Wiki), calcolarsi la spinta di Archimede sul blocco di polistirolo
    e quindi massa e densità corrette da tale effetto.
  4. Come è stato ricordato a lezione, la pressione atmosferica è dell'ordine di 105 Pa, ovvero di ≈105 N/m2.
    Da questo valore, e trascurando che il campo gravitazione diminuisce con l'altezza (ma il grosso dell'atmosfera è 'in basso'):
    1. Ricavarsi il valore approssimativo della massa di aria di una colonna di 1 m2.
    2. Ricavarsi quindi il valore approssimativo della massa di aria dell'intera atmosfera terrestre.
  5. Problema dell'ipotetico pozzo per il centro della Terra, assumendo che l'oggetto sia lasciato cadere in esso:
    1. dalle condizioni iniziali ("è lasciato cadere dalla superficie terrestre")
      x(0) = RT
      vx(0) = 0
      → si ricavino i parametri X e φ della soluzione generale (vedi sopra).
    2. Dalla x(t) ottenuta nel punto precedente si ricavino quindi:
      • vx(t);
      • ax(t).
    3. Dire per quale t l'espressione di vx(t) ha il massimo e quanto vale x in quell'istante.
      (Il risultato dovrebbe concordare con quanto ci si attende intuitivamente.)
  6. Graficare i dati simulati degli affondamento al fine di ottenere una figura 'tipo' quella riportata in Galleria
 
Torna su   —   Galleria   —   Home  
Lezione 6 (12/03, 2h)
 
Problemi proposti
  1. Calcolare periodo e velocità di rotazione di
    1. oggetto in ipotetica orbita radente intorno alla Terra;
    2. stazione orbitale ISS (per i conti si assuma un valore nominale della quota di 400 km).
  2. I satelliti geostazionari hanno la caratteristica di avere un periodo di rivoluzione intorno alla Terra
    pari a quello di rotazione della Terra sul proprio asse.
    In questo modo essi ci appaiono nel cielo sempre nella stessa posizione (vedi Galleria.)
    Valutare
    1. la loro distanza dal centro della Terra;
    2. la loro distanza dalla superficie terrestre.
  3. Calcolare la dimensione angolare con cui ci appare la stazione orbitale
    (assumendo, come ordine di grandezza, c he abbia una estensione di 100 m) quando
    1. è 'circa' allo zenit (sulla nostra testa);
    2. la vediamo a un'altezza di circa 45 gradi rispetto al piano orizzontale.
  4. Dai risultati ottenuti nel punto precedente calcolarsi, per i due casi,
    il rapporto fra la dimensione angolare della ISS e quella media della luna.
  5. Si calcolino le velocità
    • della Terra intorno al Sole (velocità media), esprimendola in km/s;
    • della Luna intorno alla Terra (velocità media), esprimendola in km/s;
    • di Roma intorno all'asse terrestre, esprimendola in km/h e m/s.
    (Per i dati orbitali necessari , in approssimazione circolare, si cerchi in rete.)
  6. Un punto materiale viaggia lungo una traiettoria rettilinea alla velocità costante di 1 m/s.
    Ad un certo istante (t0=0) esso è soggetto a una accelerazione la quale
    • cresce linearmente con il tempo e raggiunge il massimo di 1 m/s2 per t1 = 2 s;
    • da t1 decresce linearmente, fino ad annullarsi per t2 = 4 s.
    Dire, giustificando la risposta, se la velocità del punto materiale da t2 in poi
    è maggiore, minore o uguale a quella che aveva fino a t0.
    [Nota: la risposta qualitativa ben argomentata è sufficiente, ma a chi avesse
    difficoltà si raccomanda di affrontare il quesito quantitativamente,
    a partire anche da una figura che riporti l'accelerazione in funzione del tempo.]
 
Torna su   —   Galleria   —   Home  
Lezione 7 (14/03)
 
Problemi proposti
[Nota: corretto un refuso nella traccia del problema nr. 4 della lezione 6]
  1. Sulle misure (simulate) degli aumenti delle letture della bilancia in funzione
    dell'affondamento di vari solidi (vedi Galleria):
    → valutare V(x), volume affondato in funzione dell'affondamento x, e quindi Δm(x),
    massa dell'acqua spostata in funzione dell'affondamento, per
    • cilindro di raggio R;
    • prisma, avente 'altezza' h (lato che nell'affondamento è ortogonale alla superficie
      dell'acqua), base L (lato ortogonale al precedente) e spessore d;
    • cono di altezza h e raggio di base R.
    In tutti e tre i casi si troverà una legge del tipo V(x) = α·xβ
    → ricavarsi α e β nei tre casi in funzione dei parametri geometrici di ciascun solido.
  2. Si immaginino tre oggetti aventi forma di parallelepipedo e stessa massa m
    i quali formano una specie di trenino posto su un piano orizzontale privo di attrito.
    Essi sono uniti uno all'altro attraverso un filo 'inestensibile e senza peso'.
    Al primo 'vagoncino' (quello più a destra, per fissare le idee) è
    applicata una forza esterna Fext che tende a trascinare il 'trenino'.
    Si calcolino le espressioni
    1. dell'accelerazione comune con cui si muove il trenino;
    2. della tensione fra il primo e il secondo vagoncino e di quella fra il secondo e il terzo.
    Si diano quindi i risultati numerici nel caso di m = 100g e Fext=0.3N.
  3. Si ripeta il problema precedente con la variante che in cui
    fra vagoncini e piano orizzontale ci sia un attrito dinamico avente coefficiente μD=0.05.
  4. Un oggetto, a riposo su un piano orizzontale, è collegato mediante
    un filo ideale che passa su una carrucola altrettanto ideale a un oggetto sospeso,
    il quale è quindi soggetto alla forza peso e alla tensione del filo.
    1. Sapendo che la massa dell'oggetto posto sul piano vale 200 g e che il coefficiente di attrito statico vale 0.4,
      si valuti il valore massimo della massa sospesa affinché il sistema rimanga immobile.
    2. Si valuti anche, in tale situazione di equilibrio, la tensione del filo che collega i due oggetti.
  5. Con riferimento alla foto eseguita in aula e assumendo che essa mostri
    la massima inclinazione del coperchio del laptop prima che il cancellino cominci a scivolare,
    si valuti, seppur approssimativamente, il coefficiente di attrito statico fra cancellino e coperchio.
    (Riportare anche i dati utilizzati, ricavati 'alla meglio' dalla foto.)
 
Torna su   —   Galleria   —   Home  
Lezione 8 (18/03)
 
Problemi proposti
  1. Proseguimento del problema nr. 1 della Lezione nr. 6
    (e con l'ausilio di quanto ottenuto nel successivo problema nr. 3).
    • Si calcoli la velocità angolare della ISS rispetto a un osservatore
      posto sulla superficie terrestre quanto essa gli passa esattamente allo zenit
      (da non confondere con la velocità angolare dell'orbita circolare da essa compiuta intorno alla Terra!).
  2. Sul problema nr. 4 della Lezione nr. 3, il quale conteneva palesi errori di battitura
    (con velocità iniziale nulla in entrambe le coordinate i quesiti non avevano senso):
    1. Rivedere la soluzione alla luce della formulazione corretta.
    2. Riscrivere la soluzione facendo uso del modulo del vettore ('v')
      e dell'angolo che esso forma rispetto al piano orizzontale;
    3. In particolare, avendo x(t=tG) il significato di gittata e facendo uso
      della 'ben nota' formula di duplicazione 'sin(2θ) = ... '
      1. riscrivere la formula della gittata in funzione di v e di sin(2θ);
      2. trovare per quale angolo si ha la gittata massima.
  3. Sull'esperimento in aula dei lanci della moneta:
    per ciascun lancio ricavarsi:
    1. il tempo 'di volo' (da quando si stacca dal tavolo a quando tocca il pavimento);
    2. la velocità di impatto (componenti e modulo);
    3. angolo di impatto;
    4. la distanza fra il punto in cui la moneta lascia il tavolo a quello in cui tocca il pavimento
      (essa ci dà una stima per difetto della lunghezza della traiettoria).
  4. Abbiamo visto a lezione il caso di una forza costante ('mg' nell'esempio specifico)
    contrastata da una forza di 'viscosità -βv. La forza si annulla per vL=mg/β (→ 'velocità limite').
    Estendiamo il ragionamento a una forza 'attiva' costante 'FA',
    avendo quindi F = FA - βv.
    In questo caso, più generale del precedente, l'espressione della velocità limite diventa vL=FA/β.
    1. Dimostrare che, applicando il secondo principio e riscrivendo opportunamente
      i vari termini, arriviamo alla seguente equazione differenziale
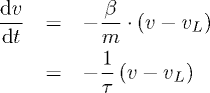
    2. Dire com'è il segno di dv/dt nei casi
      1. v > vL ;
      2. v = vL ;
      3. v < vL ,
      spiegandone il significato intuitivo.
    3. In analogia a quanto fatto a lezione nel caso di dv/dt = -v/τ
      • risolvere l'equazione differenziale usando la tecnica di separazione di variabili,
        usando come condizione iniziale v(t=0)=v0,
      • controllando che, effettivamente, la soluzione dà v(t=0)=v0 e v(t→∞)=vL.
  5. Abbiamo visto a lezione le oscillazioni di una molla quando ad essa erano sospesi 3 dischetti di piombo.
    → Dire, giustificando l'affermazione, come varia il periodo di oscillazione quando il numero di dischetti è raddoppiato.
    [Ovviamente stiamo ignorando la massa della molla stessa e del 'gancio',
    così come stiamo trascurando la resistenza dell'aria e attriti interni alla molla, per la serie "all models are wrong, ..."]
 
Torna su   —   Galleria   —   Home  
Lezione 9 (19/03)
 
Problemi proposti
  1. Si hanno 20 litri di acqua a 70 gradi. Quanta acqua fredda (10 gradi)
    bisogna aggiungere per ottenere una temperatura di equilibrio di 35 gradi?
    (Si assuma che non ci siano dispersioni di calore verso l'ambiente
    e che il contributo dei contenitori allo scambio termico sia trascurabile.)
  2. Un cilindro di 200 g di alluminio (calore specifico circa 1/5 di quello dell'acqua)
    avente una temperatura di 90 °C immerso in un recipiente contenente mezzo litro di acqua a 10 °C.
    Si trovi la temperatura di equilibrio (stesse assunzioni idealizzate del problema precedente).
  3. Calcolare la lunghezza di un pendolo semplice che 'batte il secondo'
    (ovvero ha un periodo di oscillazione di 2 s) in una località
    dove il campo gravitazionale vale esattamente 9.80 N/kg.
  4. Quanto può variare il valore calcolato nel problema precedente se in diversi punti
    della superficie terrestre g può variare al più di circa ±0.1%?
  5. Calcolare le espressioni di
    1. velocità angolare di un pendolo (da non confondere con la pulsazione 'ω'!) in funzione del tempo;
    2. velocità lungo l'arco di circonferenza percorso dal punto materiale.
    → In quale posizione esse sono massime?
    [Si consideri la soluzione particolare 'standard' in cui il pendolo a t=0
    ha l'angolo massimo rispetto alla verticale e ha velocità nulla.]
  6. Un oggetto (modellizzato come 'punto materiale') di 100 g è sospeso a un filo 'ideale' di 1 m.
    1. Si calcoli la tensione del filo quando l'oggetto penzola a riposo verticalmente.
    2. Successivamente il 'pendolo' viene fatto oscillare con un angolo massimo di 5°.
      Si calcolino, nell'istate in cui l'oggetto transita per θ=0;
      1. la sua velocità;
      2. la sua accelerazione centripeta;
      3. la forza centripeta che agisce su di esso;
      4. la tensione del filo e la si confronti con quanto ottenuto nel caso stazionario.
    [Si ricorda di seguire le raccomandazioni generali per risolvere i problemi:
    → prima arrivare alle 'formule risolutrici' e poi inserire i valori numerici dei parametri del problema.]
 
Torna su   —   Galleria   —   Home  
Lezione 10 (21/03)
 
Problemi proposti
  1. Sull'epitaffio di Stevino:
    assumendo che la 'catena' abbia densità di massa lineare costante
    dimostrare che le forze sui due piani inclinati si bilanciano esattamente.
  2. Analisi degli affondamenti dei due cilindri (vedi Galleria)
    1. riprodurre in qualche modo la figura mostrata a lezione
      tracciando le due rette passanti per l'origine e che passino 'al meglio' fra i punti sperimentali;
    2. ricavarsi i coefficienti di linearità m1 e m2 per i due cilindri;
    3. da m1 e m2 ricavarsi i diametri dei due cilindri.
  3. Analisi dell'affondamento di prisma e cono (i caso dei cilindri è da riterersi facile):
    1. linearizzare i dati di affondamento mediante opportuna trasformazione
      della variabile che quantifica l'affondamento;
    2. ricavarsi empiricamente, mediante opportuna retta che passa fra i dati,
      i coefficienti degli andamenti linearizzati;
    3. dai coefficienti ottenuti:
      1. ricavarsi, nel caso del cono, il rapporto fra raggio di base e altezza;
      2. dal valore ottenuto nel punto precedente ricavarsi l'angolo
        si 'semiapertura' del cono, ovvero fra l'asse e la superficie;
      3. ricavarsi, nel caso del prisma, il rapporto fra base e altezza,
        nell'ipotesi che lo spessore valga 2.1 cm;
      4. dal valore ottenuto nel punto precedente ricavarsi l'angolo
        al vertice del prisma.
  4. Dati i seguenti dati (non affetti da fluttuazioni dovute a errori sperimentali):
    x:  0.10 0.25 0.63 1.58 3.98 10.00
    y1: 6.32 3.99 2.52 1.59 1.00 0.63
    y2: 0.16 0.25 0.40 0.63 1.00 1.58
    y3: 0.63 1.00 1.59 2.52 3.99 6.32
    y4: 10.00 3.98 1.58 0.63 0.25 0.10
    graficare i punti su carta logaritmica ('log-log') e ricavarsi i parametri 'a' e 'b'
    delle quattro leggi di potenza yi = ai · xbi da cui essi derivano.
    (Si raccomanda di usare la carta millimetrata distribuita a lezione
    anche se può essere un utile esercizio fare i plot, ed eventualmete
    anche il resto dell'analisi, anche al computer.)
 
Torna su   —   Galleria   —   Home  
Lezione 11 (25/03)
 
Problemi proposti
  1. Sul problema nr. 15 del test di autovalutazione: è 'pacifico' che per t=190h
    l'ipotetica ninfea occupa S/2, con S la superficie dello stagno, ovvero A(t=190h)=S/2;
    così pure che A(t=180h)=S/4 e A(t=170h)=S/8, e così via, di 10 ore in 10 ore.
    La cosa più interessante è cosa succede a tempi intermedi:
    1. scrivere l'espressione di A(t), in unità di S, valida con continuità da 170 e 200 ore;
    2. verificare che per 170, 180, 190 e 200 ore si riottengono i valori che sappiamo;
    3. calcolare quanto vale A(t), sempre in unità di S, per t=175h, t=185h e t=195 h.
  2. Sulla legge di termalizzazione: trovare l'espressione, in funzione della costante di tempo τ,
    del tempo di dimezzamento 't1/2', ovvero del tempo necessario affinché la differenza
    di temperatura del corpo rispetto a quella asintotica ('TF') si dimezzi.
  3. Continuazione del problema nr. 2 Lezione 9:
    immaginiamo che acqua e alluminio raggiungano una temperatura di equilibrio
    di mezzo grado inferiore a quella che ci saremmo aspettati dai dati del problema.
    → Calcolare la capacità termica del recipiente in cui è racchiusa l'acqua;
    → dire a quanti grammi di acqua equivale.
  4. Un corpo, inizialmente a 20 °C viene immerso in un grande contenitore ('A')
    contenente acqua a 50 °C. Successivamente, dopo che si è termalizzato,
    esso viene tolto dall'acqua calda e immerso in un altresì grande recipiente ('B') di acqua a 10°.
    Assumendo che la costante di tempo ('τ') del processo di termalizzazione
    valga in entrambi i casi 60 s,
    1. si scrivano le espressioni T(t) in entrambi i casi, ponendo t=0
      nell'istante in cui il corpo è immerso in ciascuno dei recipienti;
    2. si valuti dopo quanto tempo dall'immersione esso raggiunge la temperatura di 30 °C
      1. quando è immerso nel recipiente A;
      2. quando è immerso nel recipiente B.
  5. Un cilindro di superficie di base 2 cm2 e altezza 5 cm è composto
    di un materiale avente una densità di 0.85 g/ cm3 non solubile in acqua (e tanto meno si impregna)
    Il cilindro è indrodotto in un bicchiere d'acqua e, come è ben noto, esso non affonda completamente.
    Sapendo che il bicchiere con l'acqua è posto su una bilancia e che inizialmente
    il display indicava un certo valore in grammi,
    → dire se ed eventualmente di quanto varia il valore indicato
        dal display dopo che nel bicchiere è stato introdotto il cilindro.
 
Torna su   —   Galleria   —   Home  
Lezione 12 (26/03)
 
Problemi proposti
  1. Un curioso ipotetico animale della mitologia matematica → file pdf, problema nr.1 Lezione 12.
  2. Altro simpatico quesito, da provare a risolvere in vari modi
    (la soluzione migliore è quella che richiede meno conti...):
    → 'Vecchia Dispensa', nr. 1 a pag 9.
  3. Problema nr. 2 pag. 29 'Vecchia Dispensa'.
  4. Un ipotetico eso-pianeta compie un'orbita circolare intorno al suo 'Sole'.
    Sapendo
    • che la sua distanza dal suo Sole è pari a quella nostra dal nostro Sole;
    • la sua velocità di rivoluzione è pari al doppio della nostra,
    si ricavi il rapporto fra la massa di quel 'Sole' e quella del nostro Sole.
  5. Un oggetto ('punto materiale') di massa m1=100 g che viaggia su un piano orizzontale
    privo di attrito alla velocità di 10 m/s ne urta un altro di massa m2 che stava fermo.
    Dopo l'urto i due corpi rimangono attaccatti e procedono (senza attrito!)
    lungo la direzione e il verso del corpo urtante.
    Si valuti la loro velocità nei seguenti casi:
    1. m2 = m1;
    2. m2 = 2 m1;
    3. m2 = m1/2;
    4. m2/m1 → 0;
    5. m2/m1 → ∞.
    Nei casi 1., 2. e 3. calcolarsi anche la velocità del centro di massa
    prima dell'urto e confrontarla con quella dopo l'urto.
  6. Sull'immagine del tubo a U in Galleria:
    → ricavarsi la 'sovrappressione' (rispetto a quella atmosferica) all'interno del palloncino
    → nell'ipotesi che il lato di ciascuna mattonella della parete sia 15 cm
    → e il diametro interno del tubo 1.5cm.
 
Torna su   —   Galleria   —   Home  
Lezione 13 (4/04)
 
Problemi proposti
  1. Sul problema del cagnolino (soprattutto per chi è arrivato correttamente alla soluzione
    senza passare per i dettagli indicati nel seguito), indicando con d0
    la distanza iniziale del padrone, v la sua velocità e αv quella del cagnolino.
    1. Per il primo andirivieni del cagnolino,
      1. valutare l'espressione dell'istante t1 in cui si incontrano la prima volta;
      2. la distanza (x1) dalla casa in cui si incontrano la prima volta;
      3. lo spazio (s1) per corso dal cagnolino nella sua prima andata e ritorno dalla casa.
    2. Estensione ai primi 10 andirivieni (ovviamente assumendo il cagnolino 'puntiforme', etc):
      1. estendere quando ottenuto nel punto precedente per
        ottenere l'espressione dello spazio percorso in n andirivieni
      2. usando Python, R o altro, valutarsi il percorso totale in funzione di n, usando i seguenti dati numerici:
        d0 = 100m, v = 5 km/h, α = 4.
    3. Facendosi aiutare da Wolfram Alpha o da ChatGPT ricavarsi l'espressione
      del percorso totale in funzione di d0, v e α (ovviamente il problema ha senso per α ≥ 1).
  2. Profondità del pozzo lanciando un oggetto e sentendo il rumore del tonfo
    (tempo fra rilascio e arrivo suono: 3 secondi; velocità del suono 340 m/s).
    1. Soluzione di 'ordine zero' (sempre importante!) assumendo infinita la velocità del suono.
    2. Soluzione ottenuta risolvendo l'equazione di secondo grado.
    3. Di quale problema è soluzione la soluzione spuria?
    4. Soluzione iterativa mediante Python o altro:
      • partire dalla profondità valutata in approssimazione di vs infinita;
      • sottrarre al tempo misurato il tempo impiegato dal suono per percorrere tale distanza;
      • rivalutare la profondità dal tempo ottenuto;
      • iterare il ragionamento un 'certo numero di volte' e riportare i risultati in una tabella (ordine 0, ordine 1, etc.).
  3. Valutare quanto dista dal centro della Terra il centro di massa Terra-Luna: riportare il risultato in unità di RT.
    (Prima di fare i conti si raccomanda di esprimere la massa della Luna in unità
    di masse della Terra e la distanza Terra-Luna in unità di raggi terrestri.)
  4. Dai dati delle pesate (vedi sopra) ricavarsi, per le due bottiglie, il rapporto fra la densità
    dell'aria e la densità dell'acqua, prestando attenzione alla cifre significative.
    [Nota: ovviamente i due valori dovrebbero essere identici, ma essi possono differire a causa di diversi effetti di natura sperimentale.]
  5. Dai dati del pesate delle bottiglie prima 'vuote' o poi piene di aria e assumendo,
    al fine di usare tutti gli stessi dati, P = 1025 hPa e T=22 °C,
    1. valutare il numero di moli e quindi il numero molecole di aria contenuti nelle due bottiglie;
    2. valutare il rapporto fra la densità dell'aria e la densità dell'acqua;
    3. valutare la massa media di una 'molecola di aria'.
 
Torna su   —   Galleria   —   Home  
Lezione 14 (8/04)
 
Problemi proposti
  1. Dati i due vettori a = (1, -2, 3) e b = (0, 1, 1), trovare
    1. i loro moduli;
    2. i versori corrispondenti;
    3. la loro somma;
    4. il loro prodotto scalare;
    5. l'angolo fra essi compreso.
  2. Ricavarsi, mediante calcolo dimensionale e a meno di una costante di proporzionalità numerica,
    il periodo di oscillazione di un pendolo di lunghezza l e massa sospesa m in campo gravitazionale g.
  3. Ricavarsi, mediante calcolo dimensionale e a meno di una costante di proporzionalità numerica,
    la dipendenza dello spazio di frenata dalla 'decelerazione' di modulo |a| e dalla velocità iniziale v0.
  4. Calcolare l'espressione del lavoro nei seguenti casi unidimensionali:
    1. F(x) = -m·g   [limiti: a) da x=h a x=0; b) da x=0 a x=h);
    2. F(x) = -k·x   [limiti: da x=x0 a x=0];
    3. F(x) = -k·x   [limiti: da x=0 a x=x0];
    4. F(r) = - (g/RT) r   [limiti: da r = RT a r=0];
    5. F(r) = - m·g·RT2/r2   [limiti: da r=R a r→∞ (con R ≥ RT) ];
    6. F(r) = - m·g·RT2/r2   [limiti: da r→∞ a r=R (con R ≥ RT) ];
    7. FA = -μD·m·g· v/v   [a) da x1 a x2; b) da x2 a x1]. [Nota: 'v' sta, come in molti libri di testo, per il vettore velocità, mentre 'v' per il suo modulo.)]
    Nota: il cambiamento di notazione dei nr. 5 e 6 è stato effettuato durante la lezione seguente.
 
Torna su   —   Galleria   —   Home  
Lezione 15 (9/04)
 
Problemi proposti
  1. Dati i seguenti dati (non affetti da fluttuazioni dovute a errori sperimentali)
    x:   -5.00 -2.00 1.00 4.00 7.00 10.00
    y1: 50.00 16.57 5.49 1.82 0.60 0.20
    y2: 0.50 1.05 2.19 4.57 9.56 20.00
    y3: 0.10 0.21 0.44 0.91 1.91 4.00
    y4: 5.00 2.85 1.62 0.92 0.53 0.30
    graficare i punti su carta logaritmica ('semilog') e ricavarsi i parametri 'a' e 'α'
    delle quattro leggi esponenziali yi = ai · eαi·x da cui essi derivano.
    (Si raccomanda di usare la carta millimetrata distribuita a lezione
    anche se può essere un utile esercizio fare i plot, ed eventualmete
    anche il resto dell'analisi, anche al computer.)
  2. Un punto materiale di massa 1 kg parte dall'altezza di 1 m e scivola lungo un piano inclinato
    privo di attrito e lungo sqrt(2) m (vedi Galleria).
    1. Calcolare il lavoro compiuto dalla forza peso.
    2. Calcolare la velocità finale 'vF' raggiunta, facendo uso del lavoro compiuto dalla forza peso.
  3. Ipotizziamo ora (con riferimento al problema precedente) che fra il piano inclinato
    e il punto materiale ci sia un atttrito dinamico di coefficiente μD incognito.
    → Si valuti μD dalla velocità raggiunta ('vFAD') e esprimendo il risultato
    → in funzione di r, definito come r= vFAD/vF, ovviamente minore di 1.
    → Si calcoli il valore numerico di μD nel caso di r=1/2.
  4. Un pendolo semplice di lunghezza l=1m (e con le solite idealizzazioni) è spostato
    di θ0=20° dalla posizione di equilibrio e quindi lasciato oscillare.
    Si calcolino
    1. l'innalzamento del punto materiale dalla sua quota minima
      quando l'angolo del pendolo vale θ0;
    2. usando i concetti di lavoro ed energia cinetica si valuti la velocità
      del punto materiale quando esso transita per θ=0;
    3. si calcoli quindi la corrispondente velocità angolare.
  5. Facendo uso di quando ottenuto in problemi riguardanti il pendolo di lezioni precedenti,
    si calcoli la velocità in θ=0 ottenuta facendo uso delle formule usate a suo tempo
    e valide nell' approssimazione di piccoli angoli.
    → Si confronti il risultato con quanto ottenuto nel punto 4.2.
 
Torna su   —   Galleria   —   Home  
Lezione 16 (11/04)
  Problemi proposti
(VD: 'Vecchia Dispensa':)
  1. VD, par. 10.8, nr. 4.(1)
    (Domada intermedia: ricavarsi k della molla.)
  2. VD, par. 10.8, nr. 5.(1)
  3. VD, par. 10.8, nr. 18, ove 'risultante' indica somma delle due forze.
  4. VD, par. 11.8, nr. 1.(2)
  5. VD, par. 11.8, nr. 2(2) (il lavoro richiesto va calcolato nel tratto di andata).
  6. VD, par. 13.6, nr. 2.(1)
    Note:
    • Per velocità di fuga si intende la velocità che un oggetto deve avere affinché,
      lanciato verticalmente, arrivi a distanza 'infinita' (R → ∞) con velocità nulla.
      (In pratica questo problema è una continuazione del nr. 4.5 della Lezione 14.)
    • Ovviamente si trascuri, come al solito, l'effetto dell'atmosfera.
    • Nel caso della Terra si confronti quanto ottenuto (non solo il risultato numerico!)
      con la velocità dell'altrettanto ipotetico satellite in orbita radente.
  7. Uno scaldabagno ha una potenza di 1000 W.
    → Calcolare quanto impiega a scaldare 80 litri di acqua da 10 a 60 gradi.
  8. Esperimento in aula per misurare la potenza necessaria
    per sollevare un corpo di una certa quota in un certo tempo.
    Per i dati: foto lavagna
Note:
(1) Far uso dei concetti introdotti questa settimana, senza i dettagli della cinematica;
(2) Vale nota (1) e, in particolare, usare il concetto di energia potenziale.  
Torna su   —   Galleria   —   Home  
Lezione 17 (15/04)
 
Problemi proposti
  • [1-5] Problemi nr. 1-5 delle slides.
    (Nota: problemi illustrati in aula).
  • [6] Assumendo che l'espressione dell'energia potenziale di un oggetto di massa m
    posto alla distanza R dal centro di un corpo celeste di massa M
    sia data da Ep(R) = -G·M·m/R,
    ricavarsi l'espressione della forza F(R).
    (Nota: l'espressione risultante è ben nota, ma è importante ricavarsela.)
  • [7] Un punto materiale ha una energia potenziale che dipende dalla coordinata x
    secondo la seguente espressione:
            Ep(x) = a·x2 + b·x,
    con a = 10 J/cm2 e b = - 20 J/cm.
    1. Trovare la forza che agisce sul punto materiale in funzione di x, ossia F(x).
    2. In particolare, calcolare per quale valore di x la forza si annulla.
 
Torna su   —   Galleria   —   Home  
Lezione 18 (16/04)
 
Problemi proposti
  1. Si immagini un corpo di massa m in orbita circolare intorno alla Terra.
    1. Sapendo che la forza centripeta è dovuta alla forza di gravità
      si scriva l'espressione di m·v2 in funzione dei parametri orbitali...
    2. ... e quindi si scriva l'espressione dell'energia cinetica in funzione di tali parametri.
    3. Si scriva quindi l'espressione dell'energia totale, somma dell'energia cinetica
      e dell'energia potenziale (per quest'ultima si usi lo convenzione usuale
      di porre lo zero all'infinito).
  2. Proseguimento del problema precedente:
    1. Si calcoli l'espressione dell'energia necessaria per portare tale corpo dall'orbita
      circolare di raggio R a un'orbita circolare di raggio 2R.
      [Questo concetto è simile a quello della 'eccitazione', nel quale un elettrone passa da un 'livello' a un altro.]
    2. Si calcoli l'espressione dell'energia necessaria per 'sottrarre' tale corpo alla Terra
      (ovvero di portarlo fino a distanza infinita a velocità nulla).
      [Questo concetto è simile a quello della 'ionizzazione', nel quale si sottrare un elettrone a un atomo.]
  3. Mediante un'app si misura l'illuminamento su una parete. Esso vale 150 lx.
    Successivamente si accende una torcia elettrica, posta a 5.0 m di distanza dalla parete
    e puntata ad essa ortogonalmente. La torcia proietta sulla parete un disco di luce
    'quasi omogeneo' di diametro 2.0 m. In queste condizioni l'illuminamento sale a 400 lx.
    Si calcoli il flusso luminoso emesso dalla torcia (ovviamente stiamo trascurando
    i possibili effetti di diffusione della luce della torcia nella stanza).
  4. Sul problema precedente:
    1. si valuti, seppur approsimativamente, l'angolo solido del cono del fascio luminoso
      della torcia usando, al posto della calotta sferica, la base del cono;
    2. dal flusso luminoso e dall'angolo solido calcolati nei punti precedenti
      si valuti l'intensità (media) della sorgente di luce.
  5. Immaginiamo che per fare una doccia sia necessario un flusso di acqua di 10 litri/min,
    che la temperatura di ingresso dell'acqua nella caldaia sia pari a 10 °C
    e che quella di uscita sia di 40 °C.
    Trascurando le dissipazioni termiche si valuti la potenza termica
    che deve avere la caldaia per poter fornire tale flusso di acqua calda.
    [Per avere un'idea di tale potenza si valuti a quante stufette 'caldobagno' da 2kW corrisponde.]
 
Torna su   —   Galleria   —   Home  
Lezione 19 (18/04)
 
Problemi proposti
  1. Un curioso esercizio (per il momento):
    data la funzione f(x,t) = A·cos(ω·t - β·x),
    • si calcolino le derivate seconde sia rispetto a x che rispetto a t, ovvero d2f/dx2 e d2f/dt2;
    • si mostri come ω2·d2f/dx2 è uguale a β2·d2f/dt2,
    • ... da cui segue, essendo ω2 diverso da zero, che d2f/dx2 è uguale a d2f/dt2 diviso (ω/β)2.
    Inoltre, ricordando che l'argomento della funzione coseno deve essere adimensionare,
    • dire 'che grandezza potrebbe essere' ω/β, ovvero quali sono le sue dimensioni fisiche.
  2. Facendo uso dei dati presi a lezione, valutare
    • l'angolo solido del fascio di luce del proiettore;
    • il flusso di luce che arriva sull'intero schermo;
    • l'intensità del proiettore ('sorgente di luce').
  3. Vedere sul file pdf.
  4. Vedere sul file pdf.
  5. Vedere sul file pdf.
 
Torna su   —   Galleria   —   Home  
Lezione 20 (22/04)
 
Problemi proposti
  1. Vedere sul file pdf.
  2. Vedere sul file pdf.
  3. Si immagini un pendolo balistico modellizzato come un 'pendolo semplice ideale' avente l = 1 e m = 1kg.
    Si calcoli per quale velocità un proiettile di 10g fa compiere al pendolo un'oscillazione massima di 45 gradi.
  4. Si calcolino le velocità finali dei due corpi (assumendo urti perfettamente elastici)
    per i quattro casi dell'animazione riportata in Galleria
  5. Calcolare l'angolo limite di riflessione totale quando un fascio di luce passa
    1. da acqua (n=1.33) a aria;
    2. da vetro (n=1.5) a aria.
  6. Un fascio di luce attraversa una lastra di vetro spessa 1 cm incidendo con un angolo di 45 gradi.
    Calcolare
    1. l'angolo con cui il raggio entra nel vetro;
    2. l'angolo con cui il raggio fuoriesce dalla lastra;
    3. lo spostamento laterale del raggio da prima di entrare nel vetro a quando ne esce.
 
Torna su   —   Galleria   —   Home  
Lezione 21 (23/04)
 
Problemi proposti
  1. Facendo uso di questa nuova figura
    • si scrivano le espressioni dello spazio percorso dal generico raggio luminoso
      nei due mezzi per andare da P1 a P2 in funzione di x, L, d1 e d2;
    • si scriva l'espressione del tempo totale ('t') per andare da P1 a P2 sapendo che
      le velocità nei due mezzi valgono rispettivamente v1 a v2;
    • derivando quindi l'espressione di t rispetto a x si trovi la condizione di minimo.
    A questo punto, non si tenti di risolvere rispetto a x, bensì si noti come
    l'espressione ottenuta può essere riscritta più semplicemente facendo comparire
    sinθ1 e sinθ2 (si ricordi che il seno è dato da "cateto opposto su ipotenusa"):
    → si noti la somiglianza di quanto ottenuto con la Legge di Snell;
    → si scrivano le relazioni che intercorrono fra v1 a v2 dell'espressione ottenuta e
    → n1 e n2 che compaiono nella legge di Snell.
  2. Facendo uso dei valori dell'indice di rifrazione si valuti la velocità della luce in
    • acqua;
    • aria.
  3. Abbiamo visto a lezione, benché qualitativamente, l'effetto del 'sollevamento del fondo'
    (e consequente 'accorciamento delle gambe') dovuto alla rifrazione.
    Facendo uso di questa figura che illustra più in dettaglio fenomeno
    • si valuti l'espressione del rapporto fra profondità apparente e profondità vera;
    • si riscriva l'espressione ottenuta nel limite di piccoli angoli, ovvero per θ → 0 e θ' → 0
  4. Si calcoli l'angolo limite (quello oltre il quale c'è 'riflessione totale') fra un mezzo
    di indice di rifrazione 1.500 e uno di indice di rifrazione 1.475.
    (Vedremo la ragione di questi 'curiosi valori'.)
 
Inoltre: si provi a riprodurre in Python la soluzione numerica del calcolo
del quarto di periodo di un pendolo avente angolo massimo di oscillazione arbitrario (vedi Galleria).
 
Torna su   —   Galleria   —   Home  
Lezione 22 (29/04)
 
Problemi proposti
  1. Mostrare come la funzione di energia potenziale '-GMm/R' si raccorda con 'mgh' in prossimità di R=RT.
  2. Mostrare che la somma di tante onde 'monocromatiche' Ak·cos[ k·ω0 ·(t - x/v) + φk], ciascuna avente
    • pulsazione (e quindi frequenza) multipla di una pulsazione (e quindi frequenza) fondamentale ω0 (e quindi ν0);
    • ampiezze Ak dipendenti da k;
    • sfasamenti φk dipendenti da k,
    soddisfa l'equazione di d'Alembert (ovvero è ancora un'onda).
  3. Esprimere la velocità della luce nel vuoto in centimetri al nanosecondo ('cm/ns').
  4. Usando i dati sperimentali raccolti (vedi sopra) si valuti il rapporto
    fra la velocità della luce in aria e quella in acqua.
  5. Facendo uso della relazione fra frequenza, lunghezza d'onda e velocità di propagazione (vedi sopra),
    si valuti la frequenza di onde elettromangnetiche aventi lungheza d'onda di 400 nm e di 700 nm
    (corrispondenti approssimativamente ai limiti della banda del visibile).
 
Torna su   —   Galleria   —   Home  
Lezione 23 (30/04)
 
Problemi proposti
  1. A proposito delle 'regolette di approssimazione',
    1. facendo uso dell'espansione al primo ordine (vedi lavagna di ieri) si ricavino le 'regolette' per
      1. (1 + ε)2;
      2. sqrt(1 + ε);
      3. 1/(1 + ε),
      a partire, nell'ordine, dalle seguenti funzioni:
      1. f(x) = x2;
      2. f(x) = sqrt(x);
      3. f(x) = 1/x,
      con x0=1 e 'ε = (x - x0)'.
    2. Similmente, si ricavino le 'regolette' per
      1. sin(ε);
      2. tan(ε),
      a partire, nell'ordine, dalle seguenti funzioni:
      1. f(x) = sin(x);
      2. f(x) = tan(x),
      con x0=0 e 'ε = (x - x0)'.
    3. Facendo uso dell'espansione al secondo ordine (vedi lavagna di ieri,
      nella quale xm va riscritto come xo), si ricavi la 'regoletta' per
      • cos(ε)
      a partire da
      • f(x) = cos(x),
      con x0=0 e 'ε = (x - x0)'.
  2. Ancora sull'equazione di d'Alembert:
    1. mostrare che essa è valida per la generica f(x,t) = g1(x - v·t)+ g2(x + v·t);
    2. cosa rappresentano le generiche g1(x - v·t) e g2(x + v·t)?
  3. Seguendo la traccia indicata a lezione, generalizzare il problema nr. 20.2 al caso
    in cui anche il secondo serbatoio, di sezione A2, contenga inizialmente acqua fino al livello h2
    (ovviamente stiamo ipotizzando che i due serbatoi abbiano la base allo stesso livello).
 
Torna su   —   Galleria   —   Home  
Lezione 24 (2/05)
 
Problemi proposti
  1. (Continuazione del problema nr. 1 della lezione scorsa)
    Trovare l'espansione al prim'ordine
    1. di f(x) = log(x) intorno a 1;
    2. di f(t) = e-t/τ intorno a 0.
    (Per ovvi motivi sono due casi importanti)
  2. Problema nr. 6 del par. 11.8 della Vecchia Dispensa.
  3. Problema nr. 7 del par. 11.8 della Vecchia Dispensa.
  4. In una giornata piovosa senza vento le tracce della pioggia sul finestrino
    di un treno che viaggia su un tratto pianeggiante sono inclinate rispetto alla verticale.
    Sapendo, ad esempio usando uno smart, che il treno va 60 km/h e valutando
    di 60° circa l'angolo che le tracce di pioggia formano rispetto alla verticale
    si valuti la velocità con cui scende la pioggia.
  5. Si immagini che per un ipotetico tipo di vetro i coefficienti A e B della
    cosiddetta legge di Cauchy
          n(λ) = A + B / λ2
    valgano A = 1.5 e B = 0.005 μm2.
    1. Si trovino gli indici di rifrazione per luce di 400 nm, 550 nm e 700 nm.
      [Si suggerisce di fare un plot (opzionale) al fine di visualizzare l'andamento di n(λ).]
    2. Si immagini che un fascio 'sottilissimo' di luce bianca incida con un angolo(*) di 45° 42°
      sul centro di una faccia di un grosso cubo di tale vetro, avente spigoli di 20 cm.
      Usando le tre lunghezze d'onda di riferimento indicate nel punto precedente
      si calcoli di quanto vengono 'sparpagliati' i colori del visibile quando
      la luce arriva sulla faccia opposta.
    3. Si calcoli infine il tempo (espresso in ns) impiegato dalla luce per attraversare
      il cubo di vetro (è sufficiente calcolarlo per il 'centro banda', ovvero per il verde).
    Nota: usando l'angolo di 45°, che compariva iniziamente, il raggio non arriva alla faccia opposta. Ooops...
 
Torna su   —   Galleria   —   Home  
Lezione 25 (6/05)
 
Problemi proposti
  1. Sul problema delle sei 'scatole', avendo osservato B ('black'), come a lezione:
    1. Si valuti la probabilità delle varie ipotesi, ovvero P(Hi|B,I0),
      ove 'I0' rappresenta l'informazione di background.
    2. Si valuti la probabilità di avere una pallina nera alla seconda estrazione,
      condizionata dall'osservazione di una pallina nera alla prima estrazione,
      ovvero   P(B(2)|B(1),I0).
      (Ricordiamo che la pallina estratta è stata reintrodotta nella scatola,)
  2. Si disegni una lente convergente secondo la convenzione raccomandata a lezione
    e l'asse ottico che passa al suo centro.
    Si disegni quindi un 'oggetto' situato a 6 cm dalla lente (vedi ad es. figura in Galleria).
    Sapendo che i raggi paralleli all'asse ottico convergono tutti
    in un punto sull'asse ottico a destra della lente e situato 3 cm da essa.
    1. si disegnino i tre 'raggi notevoli' che si dipartono dalla `punta' dell'oggetto;
    2. si valuti graficamente la distanza dall'immagine così ottenuta;
    3. si valuti graficamente il rapporto fra la dimensione dell'immagine
      e quella dell'oggetto.
  3. Si ripeta l'esercizio precedente nel caso in cui l'oggetto sia situato 9 cm dalla lente.
 
Torna su   —   Galleria   —   Home  
Lezione 26 (7/05)
 
Problemi proposti
  1. Con riferimento al problema delle sei scatole, indicando con pi il parametro che
    ci quantifica probabilità di ottenere una pallina bianca ('W') dalla scatola i-ma:
    Viene presa una scatola a caso e vengono eseguite 10 estrazioni con reinserimento
    ottenendo 7 volte una pallina bianca.
    1. si valuti P(pi | n, x), ovviamente uguale a P(Hi | n, x)
    2. si valuti la media, la varianza e la deviazione standard (radice quadrata della varianza)
      della distribuzione di probabilità di 'p', numero incerto che può assumere i valori pi.
  2. Continuazione dei problemi nr. 2 e 3 della lezione scorsa:
    → si calcoli i valori di q e dell'ingrandimento lineare M nei due casi
    e si confrontino i risultati con quanto ottenuto graficamente.
  3. Ancora sulla stessa lente convergente:
    1. si risolva il caso (sia graficamente che numericamente) di p = f/2;
    2. si risolva il caso (sia graficamente che numericamente) di p = f/5;
    3. si risolva il caso (sia graficamente che numericamente) di p = (3/4)*f.
  4. Ancora sulla stessa lente, ma solo soluzione numerica, assumendo y = 1 cm:
    → si valuti q, M e y' per
    1. p = (9/10)*f;
    2. p = (99/100)*f.
  5. Sul problema precedente, assumendo che l'occhio dell'osservatore sia posto a 20 cm
    dalla lente (ovviamente dalla parte opposta a dove è situato l'oggetto) e con f= 5 cm:
    1. si calcoli la dimensione angolare dell'oggetto, rispetto all'occhio,
      se la lente fosse un semplice disco di vetro;
    2. si calcoli quindi la dimensione angolare dell'immagine, sempre rispetto all'occhio, per
      1. p = (9/10)*f;
      2. p = (99/100)*f.
    3. Si calcolino infine, per i due casi di p, i rapporti fra le dimensioni angolari
      con le quali si vedono le immagini (con la lente) e quella con la quale
      si vedeva l'oggetto 'senza lente' (ovvero con un ipotetico disco di vetro).
 
Torna su   —   Galleria   —   Home  
Lezione 27 (9/05)
 
Problemi proposti
  1. Una lente di Fresnel ha una distanza focale di 17 cm (incertezza di qualche mm)
    e la parte centrale la possiamo considerare come una lente circolare di diametro d = 11.5 cm.
    1. Assumendo per il materiale un indice di 1.5 (ricordando anche quello delle fibre ottiche)
      e facendo uso della formula dei costruttori di lenti (vedi p. 41 argomentiFSN_pp35-43.pdf),
      nel caso semplice/realistico di una superficie sferica di raggio di curvatura R
      seguita da una piana (ovvero R2 → ∞ ; lenti di questo tipo si chiamano piano convesse)
      → si trovi quanto vale R.
    2. Conoscendo R e il diametro d della lente circolare equivalente
      → si valuti quanto dovrebbe essere spessa al centro una normale lente
      → (secondo la modellizzazione del punto precedente) affinché essa abbia
      → la stessa lunghezza focale della lente di Fresnel che stiamo considerando.
    Inoltre: si calcoli quante diottrie ha tale lente di Fresnel (se ne capisce meglio la 'potenza').
  2. Problema 2 sul file pdf.
  3. Si vuole far superare a un flusso d'acqua un certo dislivello.
    1. Si calcoli la differenza di potenziale gravitazionale, se il dislivello è pari a 10 m.
    2. Si calcoli la potenza della pompa necessaria a mantenere un flusso di 60 litri al minuto
      (ignorando, come al solito, attriti vari).
    3. Si calcoli inoltre a che velocità si muove l'acqua nel tubo
      che la conduce verso l'alto se esso ha un diametro interno di 2 cm.
      (Nota: l'argomento di quest'ultimo quesito non è ancora stato trattato a lezione
      ma ci si può cominciare a pensare...)
  4. Con riferimento alla batteria mostrata in Galleria:
    1. il valore '730 A' riportato sulla targhetta rappresentano la corrente massima che la batteria
      può erogare. Ovvero la sua forza elettromotrice può trasportare al massimo
      (internamente alla batteria) 730 C/s dal potenziale inferiore a quello superiore:
      → calcolare la potenza massima erogabile da tale batteria.
    2. il valore '75 Ah' sta invece per '75 A·h' e indica la carica elettrica massima
      che la batteria può portare dal potenziali inferiore a quello superiore prima
      che essa si esaurisca 'completamente'
      → calcolare il lavoro massimo che può compiere la forza elettromagnetica della batteria
      → prima che si scarichi, ovviamente equivalente all'energia totale che essa può fornire
      → e quindi a quella immagazzinata in essa.
    [Nota i valori riportati sulla batteria sono valori nominali, secondo certi standard industriali su cui
    non possiamo entrare (un po' come quando leggiamo sulle pile stilo che esse 'sono da 1.5 V', etc.).]
 
Refusi:
  • problema 17.7: Ep(r) → Ep(x);
  • problemi 16.4 e 16.5 (→ V.D. par. 11.8 nr 1 e 2):
    → chiaramente manca il valore della masse → mettere m = 1 kg.
 
Torna su   —   Galleria   —   Home  
Lezione 28 (13/05)
 
Problemi proposti
  1. Con riferimento al circuito in figura
    (uguale a quello illustrato a lezione, a parte lo scambio di f1 e f2),
    con f1 = 2.1 V, f2 = 1.9 V, R1 = 45 Ω, R2 = 10 Ω e R3 = 10 Ω;
    usando per le correnti i versi (scelti a priori!) indicati in figura:
    1. scrivere tutte le equazioni che derivano dalle Leggi di Kiechhofh;
    2. sceglierne tre indipendenti e, risolvendole, trovare I1, I2 e I3.
  2. (Continuazione del problema precedente)
    Definendo, come indicato in figura da apposito simbolo, VC = 0,
    → ricavarsi quanto valgono VA, VB e VD.
  3. (Ancora sul problema nr. 1)
    → Ricavarsi la potenza dissipata per effetto Joule da ciascun resistore.
  4. Variante A del circuito del problema nr. 1, nella quale f2 è sostituito con un filo conduttore ideale
    (il ché, per la definizione di generatore ideale di tensione, è equivalente a porre f2 = 0).
    In questo nuovo circuito R1 e R3 sono chiaramente in parallelo.
    → Si risolva il circuito usando la tecnica di riduzione a serie e paralleli,
    → chiamando I1(A), I2(A) e I3(A) le correnti ottenute.
  5. Variante B dello stesso circuito, nel quale viene posto f1 = 0,
    ottenendo così I1(B), I2(B) e I3(B) mediante la tecnica di riduzione a serie e paralleli.
  6. Si confrontino infine
    • I1, ottenute dal problema nr.1, con I1(A) + I1(B);
    • I2, ottenute dal problema nr.1, con I2(A) + I2(B);
    • I3, ottenute dal problema nr.1, con I3(A) + I3(B).
    → cosa abbiamo imparato?
 
Torna su   —   Galleria   —   Home  
Lezione 29 (14/05)
 
Problemi proposti
  1. Sul problema nr. 1 della Lezione 26 (legato alle '6 scatole'):
    → valutare P(x|n,pi)/P(x|n,pj), ove pi e pj sono due possibili valori,
    legati al contenuto delle scatole.
    (Vedremo nel seguito l'importanza di questi rapporti.)
  2. Sulla carica del condensatore in un circuito con 'f', 'R' e 'C':
    1. risolvere l'equazione differenziale a cui siamo giunti: → VC(t) , Q(t);
    2. ricordando che I = dQ/dt, trovare la corrente che circola nel circuito
      durante il processo di carica;
    3. facendo uso della Legge di Ohm trovare quindi l'espressione di VR(t).
  3. (Continuazione del problema precedente):
    → trovare l'espressione dell'energia erogata dal generatore durante il processo di carica.
  4. (Ancora continuazione del problema nr. 2):
    1. dall'espressione di I(t) si derivi l'espressione di 'PJ(t)',
      potenza (istantanea) dissipata per effetto Joule dal resistore;
    2. integrando PJ(t) da t=0 a t→∞ si ricavi l'espressione dell'energia totale dissipata
      per effetto Joule dal resistore durante l'intero processo di carica del condensatore.
  5. Confrontando i risultati ottenuti nei problemi nr. 3 e 4 si faccia il bilancio energetico.
 
Torna su   —   Galleria   —   Home  
Lezione 30 (16/05)
 
Problemi proposti
  1. Vedi problema nr. 1 sul file pdf.
  2. Vedi problema nr. 2 sul file pdf.
  3. Vedi problema nr. 2 sul file pdf.
  4. Risolvere il circuito del problema 28.1 usando il metodo matriciale.
    (Usare R, Python, Julia o altro → proibito fare i conti a mano!)
  5. In analogia ai problemi della lezione scorsa, risolvere il circuito 'RC' per il processo di scarica.
    In particolare:
    1. trovare l'espressione di VC(t);
    2. trovare l'espressione di I(t) e quindi, banalmente, di VR(t);
    3. trovare l'energia dissipata per effetto Joule durante l'intero processo di scarica:
      → cosa abbiamo imparato?
 
Torna su   —   Galleria   —   Home  
Lezione 31 (20/05)
 
Problemi proposti
  1. Premesse (senza vere dimostrazioni):
    • Per i condensatori in serie e parallelo valgono le regole opposte
      a quelle dei resistori. In particolare, per il parallelo, vale Cp = C1 + C2.
    • Se due condensatori hanno cariche rispettivamente Q1 e Q2, quando essi
      sono successivamente posti in parallelo (e isolati dal 'resto del mondo')
      la carica totale Q1 e Q2 si distribuirà sul condensatore equivalente di capacità Cp.
    Con queste informazioni e assumendo C1 = 1 μF, C2 = 10 μF, VC1 = 1 V e VC2 = 5 V, valutare
    1. l'energia immagazzinata inizialmente da ciascun condensatore;
    2. l'energia immagazzinata del sistema dei due quando essi sono
      successivamente collegati in parallelo;
    3. la variazione di energia fra la configurazione iniziale e quella finale.
    Ci ricorda qualcosa?
  2. Continuazione del problema nr. 4 della lezione scorsa:
    modificare il vettore colonna dei coefficienti (ove compaiono f1 e f1) e operare le seguenti varianti:
    1. porre f1=0 e risolvere per I1, I2 e I2;
    2. idem, ponendo (soltanto!) f2=0.
    ↠ Si confrontino le soluzioni con quanto ottenuto quando entrambe le f.e.m. erano diverse da zero.
    [Il cosidetto 'principio' di sovrapposizione è una diretta consequenza della linearità delle equazioni dei circuiti!]
  3. Vedi problema nr. 3 sul file pdf.
  4. Vedi problema nr. 4 sul file pdf.
  5. Vedi problema nr. 5 sul file pdf.
 
Torna su   —   Galleria   —   Home  
Lezione 32 (21/05)
 
Problemi proposti
  1. Vedi problema nr. 1 sul file pdf.
  2. Vedi problema nr. 2 sul file pdf.
  3. Vedi problema nr. 3 sul file pdf.
  4. Vedi problema nr. 4 sul file pdf.
  5. Vedi problema nr. 5 sul file pdf.
  6. Continuare l'analisi dei lanci della moneta al fine di valutare
    la lunghezza della traiettoria percorsa.
 
Torna su   —   Galleria   —   Home  
Lezione 33 (23/05)
 
Problemi proposti
  1. Vedi problema nr. 1 sul file pdf.
  2. Vedi problema nr. 2 sul file pdf.
 
Torna su   —   Galleria   —   Home  
Lezione 34 (27/05)
 
Problemi proposti
  1. Continuazione del problema nr. 32.1:
    1. Quanto vale la probabilità, secondo il 'Fisico 1', di osservare nuovamente n=0
      dopo che precedentemente era stato osservato n=0?
    2. E se precedentemente fosse stato osservato n=1?
    Inoltre:
        3. cosa penserà invece il 'Fisico 2' (→ problema nr 32.2), a parità di osservazioni empiriche?
  2. Continuare il calcolo, impostato a lezione, del momento di inerzia di una barra
    rispetto al generico punto (anche esterno ad essa) passante per il suo asse.
  3. Un ipotetico pianeta ha un'orbita tale per cui la sua distanza dal suo Sole
    al perielio vale esattamente la metà di quando si trova all'afelio.
    • Sapendo che all'afelio la sua velocità vale 20 km/s, facendo uso della conservazione
      del momento della quantità di moto si valuti la velocità al perielio.
  4. Problema nr. 4 del par. 36.3 di argomentiFSN_pp65-72.pdf.
 
Torna su   —   Galleria   —   Home  
Lezione 35 (30/05)
 
Problemi proposti
  1. Completare il calcolo del momento di inerzia di una sfera intorno al proprio asse.
  2. Risolvere il quesito sulla foto del cartello dell'Aula Pasquini.
  3. Sulla stessa foto: si calcoli la grandezza angolare (espressa in gradi e
    sue frazioni, ovvero primi e secondi d'arco)
    1. dell'intero cartello;
    2. del rettangolo che rappresenta l'estintore;
    3. nella lettera N di ESTINTORE.
 
Torna su   —   Galleria   —   Home  
Lezione 36 (3/06)
 
Problemi proposti
  1. Analisi di un pendolo costituito da una sfera di raggio R, sospesa a un filo
    di lunghezza l (dal punto di sospensione al centro della sfera).
    In analogia con quanto fatto per la barra oscillante, trovare le espressioni di
    1. momento di inerzia rispetto al punto di sospensione;
    2. momento della forza peso rispetto al punto di sospensione;
    3. equazione differenziale che descrive il moto del pendolo;
    4. suo sviluppo per θ 'piccolo';
    5. lunghezza equivalente (leq) di tale pendolo, ovvero la lunghezza di un
      pendolo semplice ideale che ha lo stesso periodo di oscillazione;
    6. periodo di tale pendolo e suo rapporto rispetto a quello di un pendolo
      semplice ideale di lunghezza l.
  2. Uno smart ha il sensore di 4.54mm×3.42mm.
    Si calcoli
    1. la lunghezza focale ('f') che lo smart usa per avere un'apertura di
      di campo orizzontale di 40°.
    2. la lunghezza focale che invece si usa con una fotocamera 'full frame'
      per avere la stessa apertura di campo.
    3. il rapporto (maggiore su minore) fra le due lunghezze focali.
  3. Al fine di avere foto 'ben esposte' un fotografo sta usando f/5.6 e T=1/60 s
    (a lezione 'T'era stato indicato con 'ΔT'; il numero di diaframma,
    che qui vale 5.6, era stato indicato con nD).
    Improvvisamente passa una leggera nuvola e il flusso di luce che arriva
    all'ingresso dell'obiettivo si riduce a un quarto di quello precedente.
    1. Come dovrà essere modificato il 'numero di diaframma' se il fotografo
      vuole mantenere lo stesso tempo di esposizione?
    2. Come dovrà cambiare invece il tempo di esposizione se vuole
      mantenere lo stesso numero di diaframma?
    3. Quali sono, qualitativamente, i pro e contro delle due opzioni?
    [Nota: ovviamente il fotografo potrebbe aumentare anche la sensibilità,
    quadruplicando 'gli ISO' (come si dice colloquialmente), ma questa opzione
    riduce la qualità dell'immagine (come ben noto, le decisioni sono spesso
    compromessi fra le diverse opzioni)]
  4. Nella dimostrazione in aula è stato fatto uso di un puntatore laser blu
    (un po' sul viola) la cui luce aveva una lunghezza d'onda di 400 nm.
    Il reticolo di diffrazione aveva invece 600 linee/mm (vedi foto).
    Supponiamo inoltre che il fascetto di luce fosse diretto verso il reticolo
    orizzontalmente e perfettamente normale a esso.
    1. Si calcolino i primi due angoli (a destra) a cui veniva deviato il fascetto di luce.
    2. Supponendo inoltre che la distanza fra reticolo e parete valesse due metri
      si calcolino le distanze fra il punto luminoso prodotto dal fascetto non deflesso
      e quelli degli altri due punti luminosi.
 
Torna su   —   Galleria   —   Home  
Torna alla pagina del corso