The heuristic rule resulting from the discussion is
where 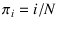 , with
, with 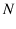 the total number of balls in box
the total number of balls in box 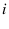 ,
is the white ball proportion and
,
is the white ball proportion and
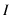 stands for
all other available information regarding the experiment.
[In the sequel we shall use the shorter notation
stands for
all other available information regarding the experiment.
[In the sequel we shall use the shorter notation
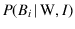 in place of
in place of
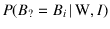 ,
keeping instead always explicit the `background' condition
,
keeping instead always explicit the `background' condition 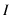 .]
But, since the probability
.]
But, since the probability
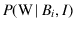 of getting White from box
of getting White from box 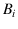 is trivially
is trivially 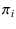 (we shall come back to the reason) we get
(we shall come back to the reason) we get
This rule is obviously not general, but depends on the fact
that we initially considered all boxes equally likely,
or
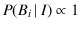 , a convenient notation in place
of the customary
, a convenient notation in place
of the customary
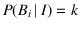 , since common factors are irrelevant.
So a reasonable ansatz for the updating rule,
consistent with the result of the discussion, is
, since common factors are irrelevant.
So a reasonable ansatz for the updating rule,
consistent with the result of the discussion, is
But if this is the proper updating rule, it has to hold after
the second extraction too, i.e. when 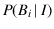 is replaced by
is replaced by
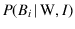 , which we rewrite as
, which we rewrite as
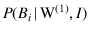 to make it clear that such a
probability depends also on the
observation of White in the first extraction. We have then
to make it clear that such a
probability depends also on the
observation of White in the first extraction. We have then
and so on. By symmetry, the updating rule in case Black (`B')
were observed is
with
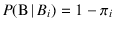 . After a sequence of
. After a sequence of 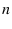 White
we get therefore
White
we get therefore
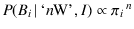 . For example
after 20 White we are - we must be! -
98.9% confident to have chosen
. For example
after 20 White we are - we must be! -
98.9% confident to have chosen 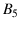 and 1.1%
and 1.1%
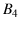 , with the remaining possibilities `practically'
ruled out.
, with the remaining possibilities `practically'
ruled out.![[*]](footnote.png)
If we observe, continuing the extractions,
a sequence of 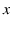 White
and
White
and 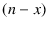 Black we get
Black we get![[*]](footnote.png)
But, since there is a one-to-one relation between 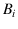 and
and 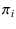 ,
we can write
,
we can write
an apparently `innocent' expression on which we shall comment later.
![[*]](footnote.png)
![]() White
and
White
and ![]() Black we get
Black we get![[*]](footnote.png)