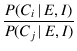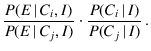As a matter of fact, the above updating rule can be shown to result
from probability theory, and I find it magnificently
described in simple words by Laplace in what he calls
“the fundamental principle
of that branch of the analysis of chance
that consists of reasoning a posteriori from events
to causes” (2):![[*]](footnote.png)
“The greater the probability of an observed event given any one
of a number of causes to which that event may be attributed,
the greater the likelihood
of that cause {given that event}.
The probability of the existence of any one of these causes
{given the event} is thus a fraction
whose numerator is the probability of the event given the cause,
and whose denominator is the sum of similar probabilities,
summed over all causes. If the various causes are not equally probable
a priori, it is necessary, instead of the probability of the event
given each cause, to use the product of this probability
and the possibility
of the cause itself.” (2)
Thus, indicating by 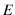 the effect and by
the effect and by 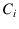 the
the 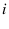 -th cause,
and neglecting normalization, Laplace's
fundamental principle is as simple as
-th cause,
and neglecting normalization, Laplace's
fundamental principle is as simple as
from which we learn a simple rule that teaches us how
to update the ratio of probabilities we assign to
two generic causes 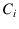 and
and 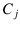 (not necessarily mutually exclusive):
(not necessarily mutually exclusive):
Equation (8) is a convenient way to
express the so-called Bayes rule (or `theorem'), while the
last one shows explicitly how the ratio of the probabilities of two causes
is updated by the piece of evidence 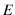 via the so called
Bayes factor (or Bayes-Turing factor (3)).
Note the important implication
of Equation (8): we cannot update the probability of a cause,
unless it becomes strictly falsified, if we not consider
at least another fully specified cause (5,4).
via the so called
Bayes factor (or Bayes-Turing factor (3)).
Note the important implication
of Equation (8): we cannot update the probability of a cause,
unless it becomes strictly falsified, if we not consider
at least another fully specified cause (5,4).
![[*]](footnote.png)