Coming to the probability of White in the second extraction,
it is now clear why
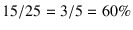 is wrong: it assumed
the remaining five boxes equally
likely,
is wrong: it assumed
the remaining five boxes equally
likely,![[*]](footnote.png) while they are not.
Also in this case maieutics helps: it becomes suddenly
clear that we have to assign a higher `weight' to the compositions
we consider more likely. That is, in general and remembering that
the weights
while they are not.
Also in this case maieutics helps: it becomes suddenly
clear that we have to assign a higher `weight' to the compositions
we consider more likely. That is, in general and remembering that
the weights 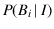 sum up to unity,
sum up to unity,
After the observation of White in the first
extraction we then get![[*]](footnote.png)
where
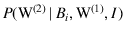 has been rewritten
as
has been rewritten
as
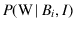 since, assuming a particular composition,
the probability of White is the same in every extraction.
Moreover,
since
since, assuming a particular composition,
the probability of White is the same in every extraction.
Moreover,
since
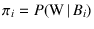 ,
we can rewrite Equation (11), in analogy with
Equation (7), i.e. replacing
,
we can rewrite Equation (11), in analogy with
Equation (7), i.e. replacing 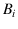 by
by 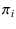 ,
as
,
as
which will deserve comments later.
![[*]](footnote.png) while they are not.
Also in this case maieutics helps: it becomes suddenly
clear that we have to assign a higher `weight' to the compositions
we consider more likely. That is, in general and remembering that
the weights
while they are not.
Also in this case maieutics helps: it becomes suddenly
clear that we have to assign a higher `weight' to the compositions
we consider more likely. That is, in general and remembering that
the weights ![[*]](footnote.png)