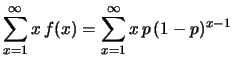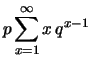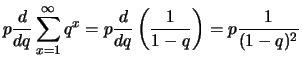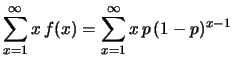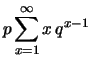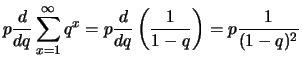Distribuzione geometrica

Questa volta il calcolo è meno banale:

$$(X\,\vert\,{\cal G}_p) = \sum_{x=1}^\infty x\,f(x) = \sum_{x=1}^\infty x\, p\,(1-p)^{x-1}$$

$$= p\sum_{x=1}^\infty x\,q^{x-1}$$

$$= p\frac{d}{dq}\sum_{x=1}^\infty q^{x} = p\frac{d}{dq}\left(\frac{1}{1-q}\right)=p\frac{1}{(1-q)^2}$$

$$= \frac{1}{p}\,.$$ (6.32)

Per i casi della moneta, del dado, dell'ubriaco con le 8 chiavi e del singolo estratto al lotto otteniamo rispettivamente delle previsioni di 2, 6, 8 e 18 prove. Questo sta ad indicare che la risposta intuitiva ``mi aspetto un successo ogni 2 (o 6, 8, 18) estrazioni'' faceva riferimento a questo concetto.