Next: Distribuzione geometrica
Up: Deviazione standard delle distribuzioni
Previous: pzd100 Distribuzione uniforme di
Indice
La semplicità della distribuzione di Bernoulli permette
di calcolare la varianza in due modi diversi, come media (pesata)
dei quadrati degli scarti o come media dei quadrati meno il
quadrato della media:
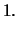 Var Var |
 |
E![$\displaystyle [(X-\mu)^2]$](img1120.png) |
|
| |
 |
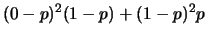 |
|
| |
 |
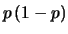 |
(6.45) |
| |
|
|
|
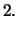 Var Var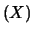 |
 |
E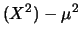 |
|
| |
 |
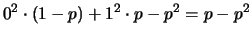 |
|
| |
 |
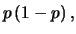 |
(6.46) |
| ovvero |
|
|
|
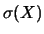 |
 |
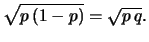 |
(6.47) |
L'incertezza di previsione è massima quando
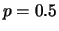 e, in tale caso, assume il valore della previsione stessa.
Per
e, in tale caso, assume il valore della previsione stessa.
Per  che tende a 0 o a 1 la deviazione standard tende a 0.
Per quanto riguarda il coefficiente di variazione abbiamo:
che tende a 0 o a 1 la deviazione standard tende a 0.
Per quanto riguarda il coefficiente di variazione abbiamo:
Esso indica che l'incertezza di previsione relativa
tende a zero per  prossimo a 1, mentre diverge
come
prossimo a 1, mentre diverge
come
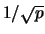 per
per  molto piccolo.
molto piccolo.




Next: Distribuzione geometrica
Up: Deviazione standard delle distribuzioni
Previous: pzd100 Distribuzione uniforme di
Indice
Giulio D'Agostini
2001-04-02