



Next: Processo di Bernoulli e
Up: Deviazione standard delle distribuzioni
Previous: Processo di Bernoulli
Indice
In questo caso il calcolo della varianza è meno semplice
di quelli precedenti. Diamo
direttamente il risultato:
Quindi, se  è abbastanza piccola, l'incertezza di previsione
è circa pari alla previsione stessa. Il coefficiente di
variazione vale
è abbastanza piccola, l'incertezza di previsione
è circa pari alla previsione stessa. Il coefficiente di
variazione vale
indicando un'incertezza percentuale di previsione che tende al 100%
per  piccolo.
piccolo.
Nel caso del singolo estratto al lotto (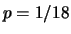 )
l'incertezza standard di previsione vale 17.5 settimane a fronte
di una previsione di 18. Tenendo conto inoltre della forma
fortemente asimmetrica della distribuzione, ci capisce come
enormi ritardi rispetto alla frequenza media siano da ritenere
niente affatto ``sorprendenti''. Nel caso del lancio di una
moneta regolare ci si aspetta invece di ottenere un certo
esito per la prima volta dopo 2 lanci, con un'incertezza di
1.4. Si vede quindi come, in effetti, la deviazione standard
fornisca una misura dell'incertezza di previsione
migliore di quella ottenibile facendo uso
dell'intervallo di variabilità della variabile, così come
il baricentro della distribuzione rende meglio l'idea di previsione
del valore di massima probabilità.
)
l'incertezza standard di previsione vale 17.5 settimane a fronte
di una previsione di 18. Tenendo conto inoltre della forma
fortemente asimmetrica della distribuzione, ci capisce come
enormi ritardi rispetto alla frequenza media siano da ritenere
niente affatto ``sorprendenti''. Nel caso del lancio di una
moneta regolare ci si aspetta invece di ottenere un certo
esito per la prima volta dopo 2 lanci, con un'incertezza di
1.4. Si vede quindi come, in effetti, la deviazione standard
fornisca una misura dell'incertezza di previsione
migliore di quella ottenibile facendo uso
dell'intervallo di variabilità della variabile, così come
il baricentro della distribuzione rende meglio l'idea di previsione
del valore di massima probabilità.




Next: Processo di Bernoulli e
Up: Deviazione standard delle distribuzioni
Previous: Processo di Bernoulli
Indice
Giulio D'Agostini
2001-04-02
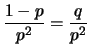
![$\displaystyle \frac{\sqrt{q}}{p} \xrightarrow[p\rightarrow 0]{}\frac{1}{p}
=$](img1182.png) E
E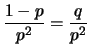
![$\displaystyle \frac{\sqrt{q}}{p} \xrightarrow[p\rightarrow 0]{}\frac{1}{p}
=$](img1182.png) E
E![$\displaystyle \frac{\sqrt{q/p}}{1/p} = \sqrt{q}\xrightarrow[p\rightarrow 0]{}1\,,$](img1183.png)
![]() )
l'incertezza standard di previsione vale 17.5 settimane a fronte
di una previsione di 18. Tenendo conto inoltre della forma
fortemente asimmetrica della distribuzione, ci capisce come
enormi ritardi rispetto alla frequenza media siano da ritenere
niente affatto ``sorprendenti''. Nel caso del lancio di una
moneta regolare ci si aspetta invece di ottenere un certo
esito per la prima volta dopo 2 lanci, con un'incertezza di
1.4. Si vede quindi come, in effetti, la deviazione standard
fornisca una misura dell'incertezza di previsione
migliore di quella ottenibile facendo uso
dell'intervallo di variabilità della variabile, così come
il baricentro della distribuzione rende meglio l'idea di previsione
del valore di massima probabilità.
)
l'incertezza standard di previsione vale 17.5 settimane a fronte
di una previsione di 18. Tenendo conto inoltre della forma
fortemente asimmetrica della distribuzione, ci capisce come
enormi ritardi rispetto alla frequenza media siano da ritenere
niente affatto ``sorprendenti''. Nel caso del lancio di una
moneta regolare ci si aspetta invece di ottenere un certo
esito per la prima volta dopo 2 lanci, con un'incertezza di
1.4. Si vede quindi come, in effetti, la deviazione standard
fornisca una misura dell'incertezza di previsione
migliore di quella ottenibile facendo uso
dell'intervallo di variabilità della variabile, così come
il baricentro della distribuzione rende meglio l'idea di previsione
del valore di massima probabilità.