



Next: Problemi
Up: Variabili casuali e distribuzioni
Previous: Misure di centralità e
Indice
- Un numero aleatorio (o variabile casuale) rappresenta
un numero ben definito, ma rispetto al quale
si è in stato di incertezza.
- Quando a ciascun possibile valore del numero aleatoria
si associa un grado di fiducia si costruisce una
distribuzione di probabilità. Nel caso di variabili discrete
la funzione di probabilità
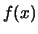 ha il significato
di probabilità che la variabile
ha il significato
di probabilità che la variabile  assuma il valore
assuma il valore  .
.
- Le proprietà delle funzioni di probabilità discendono direttamente
dalle proprietà della probabilità.
- Quando si hanno invece valori numerici associati alla frequenza
con il quale essi si sono verificati nel passato si parla di distribuzione
statistica.
- La distribuzione che assegna pari probabilità a tutti i possibili valori
di una variabile casuale è la distribuzione uniforme. In questo
capitolo sono state mostrate soltanto quelle più semplici con
valori della variabile casuale equidistanziati.
- Nel processo di Bernoulli si definisce una variabile pari all'indicatore
del contenuto di verità di un evento. Considerando più processi
di Bernoulli indipendenti e definiti su eventi analoghi
aventi tutti la stessa probabilità si ottengono altre distribuzioni
di notevole interesse. In particolare, la distribuzione geometrica
è legata numero di processo di Bernoulli nel quale si verifica
per la prima volta un evento favorevole.
- Sebbene la distribuzione di probabilità descriva completamente lo stato
di incertezza ripetto al numero aleatorio, è molto pratico
poter riassumere le aspettative sul verificarsi del numero in termini
di previsione (il valore intorno
al quale si verificherà ragionevolmente la variabile casuale)
e di incertezza di previsione (caratterizzata dalla dispersione
dei possibili valori intorno alla previsione).
- È conveniente utilizzare,
come definizione
operativa di previsione,
la media dei valori che il numero aleatorio può assumere,
ciascuno pesato con
grado di fiducia che gli si attribuisce (baricentro
della distribuzione).
- Valore atteso, valore aspettato, speranza matematica,
(valore di aspettazione) e media sono da considerare sinonimi
di previsione.
Si noti inoltre che il concetto di previsione non va confuso
né con quello di valore di massima probabilità (detto moda)
né con quello centrale (detto mediana) che divide i valori
della variabile casuale in due classi ordinate di pari probabilità.
- Il modo ``standard'' di quantificare l'incertezza di previsione
consiste nel fare uso
della previsione dei quadrati degli scarti rispetto alla
previsione stessa.
Questo indicatore di dispersione è chiamato varianza.
Per convenienza si usa la
la radice quadrata della varianza,
detta deviazione standard,
grandezza omogena con la variabile di interesse e con la
previsione e quindi più facilmente percepibile.
- Anche le distribuzioni statistiche possono essere sintetizzate
con misure di centralità e di dispersione analoghe
a quelle delle distribuzioni di probabilità.
Spesso nella letteratura scientifica alcuni termini e simboli
vengono spesso usati
pressoché indistintamente per le due distribuzioni.
È opportuno abituarsi ad una certa flessibilità di simbologia,
a capire dal contesto qual'è il significato esatto da attribuire
alle grandezze e, infine, a chiarire cosa a cosa ci si voglia riferire
se non è univoco dal contesto.




Next: Problemi
Up: Variabili casuali e distribuzioni
Previous: Misure di centralità e
Indice
Giulio D'Agostini
2001-04-02