



Next: Distribuzioni triangolari
Up: pzd100Simulazione al computer di
Previous: Scelta pesata con
Indice
Uno dei metodi più universali di estrazione, valido anche per
variabili casuali definite in un dominio infinito, fa uso
della funzione di ripartizione.
Cominciamo con variabili discrete, ricordandoci
della rappresentazione grafica ``a gradini'' della
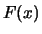 (vedi figura 6.3). Per ogni valore
(vedi figura 6.3). Per ogni valore 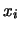 in cui
in cui
 è definita, il ``salto'' da un gradino all'altro
è pari a
è definita, il ``salto'' da un gradino all'altro
è pari a 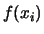 .
Se si estrae un numero casuale
.
Se si estrae un numero casuale 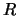 fra 0 e 1
e lo si posiziona lungo l'asse delle ordinate
del grafico di
fra 0 e 1
e lo si posiziona lungo l'asse delle ordinate
del grafico di 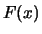 si ha che
si ha che
Quindi questa procedura permette di ottenere valori di
 la cui probabilità di verificarsi è data dalla
distribuzione di interesse.
la cui probabilità di verificarsi è data dalla
distribuzione di interesse.
Per passare alle variabili continue basta pensare
al limite di una funzione a gradini, con infiniti gradini
talmente ravvicinati e di salto infinitesimo
d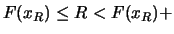 d
d .
Ancora una volta si vede come il
grado di fiducia con cui i possibili valori di
.
Ancora una volta si vede come il
grado di fiducia con cui i possibili valori di  possono essere sorteggiati è proporzionale a
possono essere sorteggiati è proporzionale a 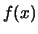 .
Così pure, in analogia al caso discreto,
si può dire che, se
.
Così pure, in analogia al caso discreto,
si può dire che, se
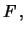
d
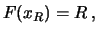
ovvero se
il gradino infinitesimo è quello in corrispondenza di 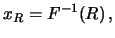 .
Questo metodo, applicato alle variabili continue la
cui funzione densità di probabilità è integrabile
analiticamente
e la
.
Questo metodo, applicato alle variabili continue la
cui funzione densità di probabilità è integrabile
analiticamente
e la 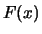 facilmente invertibile, è senz'altro il più rapido,
in quanto:
ove
facilmente invertibile, è senz'altro il più rapido,
in quanto:
ove
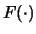 sta per l'inversa di
sta per l'inversa di  .
.




Next: Distribuzioni triangolari
Up: pzd100Simulazione al computer di
Previous: Scelta pesata con
Indice
Giulio D'Agostini
2001-04-02
![]() (vedi figura 6.3). Per ogni valore
(vedi figura 6.3). Per ogni valore ![]() in cui
in cui
![]() è definita, il ``salto'' da un gradino all'altro
è pari a
è definita, il ``salto'' da un gradino all'altro
è pari a ![]() .
Se si estrae un numero casuale
.
Se si estrae un numero casuale ![]() fra 0 e 1
e lo si posiziona lungo l'asse delle ordinate
del grafico di
fra 0 e 1
e lo si posiziona lungo l'asse delle ordinate
del grafico di ![]() si ha che
si ha che
![]() d
d![]() .
Ancora una volta si vede come il
grado di fiducia con cui i possibili valori di
.
Ancora una volta si vede come il
grado di fiducia con cui i possibili valori di ![]() possono essere sorteggiati è proporzionale a
possono essere sorteggiati è proporzionale a ![]() .
Così pure, in analogia al caso discreto,
si può dire che, se
.
Così pure, in analogia al caso discreto,
si può dire che, se
 .
.