Per ragioni di convenienza legate alle applicazioni che
incontreremo, consideriamo una variabile casuale che abbia
il significato di tempo ![]() . È anche opportuno utilizzare un
parametro omogeneo con
. È anche opportuno utilizzare un
parametro omogeneo con ![]() indicato con
indicato con ![]() (
(![]() ).
Si ottiene
allora la seguente espressione per la
distribuzione esponenziale nel dominio del tempo:
).
Si ottiene
allora la seguente espressione per la
distribuzione esponenziale nel dominio del tempo:
Calcoliamoci il valore atteso e deviazione standard di ![]() :
:
E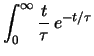 |
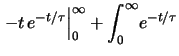 |
||
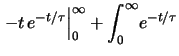 |
|||
E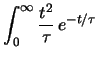 |
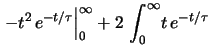 d d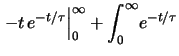 |
||
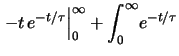 |
|||
 |
La distribuzione esponenziale può essere atta a descrivere una situazione di incertezza in cui anche valori molto grandi della grandezza possono essere ammissibili, ma con gradi di fiducia tali che dopo alcune deviazioni standard si è ``praticamente certi'' che essi non si verifichino. Un caso interessantissimo in cui essa entra in gioco è nei tempi di attesa di conteggi in fenomeni descritti da processi di Poisson (vedi paragrafo 8.12 nel prossimo paragrafo.