



Next: Variabili casuali doppie discrete
Up: Variabili casuali multiple
Previous: Variabili casuali multiple
Indice
Nei capitoli precedenti abbiamo considerato un numero aleatorio
alla volta, introducendo il formalismo generale per descrivere
lo stato di incertezza rispetto. Come si può bene immaginare,
nei casi reali ci si trova
spesso a dover considerare più grandezze dai valori incerti.
Facciamo degli esempi.
- Consideriamo 100 lancio consecutivi di una moneta. Si può essere interessati
al numero di teste, al numero di croci, al numero più elevato di teste
consecutive che si è verificato e al numero di cambiamenti
di esito (ogni volta che dopo un certo numero di teste è uscita
croce e viceversa). Quali risultati sarà possibile ottenere?
{0, 0, 0, 0},
{1, 0, 0, 0}, ...
{50, 50, 1, 49},
...
{100, 100, 100, 100}? (Con
``{...}" è indicata la lista ordinata
dei valori numerici di ciascuna delle
variabili di interesse. Molte di queste combinazioni risultano impossibili.)
- Scelgo uno studente a caso che abbia terminato tutti
gli esami del corso. Che voti ha riportato in ciascuno degli esami?
{18, 18, 18, ..., 18},
{19, 18, 18, ..., 18}, ...,
{30, 30, 30, ..., 30}? (Con ``{...}" è indicata
la lista dei possibili risultati,
ordinata per ordine alfabetico degli esami.)
- Si lancia una pallina su un tavolo
di
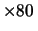 cm
cm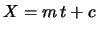 cm?
In quale punto del piano si fermerà?
{0.0, 0.0},
{0.0, 0.1},
{0.1, 0.1},
...
{120.0, 80.0},
(discretizzando al millimetro le
coordinate, prese a partire da uno spigolo)
cm?
In quale punto del piano si fermerà?
{0.0, 0.0},
{0.0, 0.1},
{0.1, 0.1},
...
{120.0, 80.0},
(discretizzando al millimetro le
coordinate, prese a partire da uno spigolo)
- La legge fisica che lega la grandezza
 (misurata in unità arbitrarie)
al tempo è del tipo
(misurata in unità arbitrarie)
al tempo è del tipo
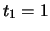 . Se
. Se 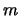 e
e 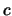 valgono rispettivamente 3 e di 1
(unità arbitrarie) e la misura è affetta da errori
casuali, quali valori
di
valgono rispettivamente 3 e di 1
(unità arbitrarie) e la misura è affetta da errori
casuali, quali valori
di 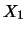 e di
e di 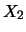 (misurati con ``strumenti reali'')
si osserveranno ai tempi
(misurati con ``strumenti reali'')
si osserveranno ai tempi 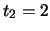 e
e 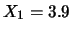 ?
{3.7, 6.7},
{3.8, 6.7}, ...
{4.0, 7.0}, ...
{4.5, 7.5}?
?
{3.7, 6.7},
{3.8, 6.7}, ...
{4.0, 7.0}, ...
{4.5, 7.5}?
- Caso inverso del precedente: avendo osservato
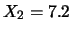 e
e 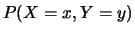 ai tempi
ai tempi
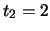 e
e 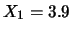 , cosa si può dire sui
``valori veri''
dei coefficienti
, cosa si può dire sui
``valori veri''
dei coefficienti 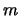 e
e 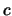 ?
{3.1, 0.4},
...
{3.3, 0.6},
...
{3.4, 0.5}?
?
{3.1, 0.4},
...
{3.3, 0.6},
...
{3.4, 0.5}?
Ricapitolando, in generale si è in stato
di incertezza rispetto alla realizzazione di  variabili casuali,
o , come si dice,
rispetto a un vettore aleatorio di
variabili casuali,
o , come si dice,
rispetto a un vettore aleatorio di  componenti,
anche chiamato
componenti,
anche chiamato  -tupla (leggi ``entupla")
di valori.
-tupla (leggi ``entupla")
di valori.
Come al solito, lo stato di incertezza su ciascun possibile
vettore aleatorio sarà quantificato
da un grado di fiducia.
Vediamo separatamente il caso
discreto e quello continuo. Successivamente,
molte delle proprietà
saranno descritte in modo generale per i due casi, eventualmente
scegliendo variabili discrete o continue per gli esempi, a
seconda di quella che meglio si presta
al caso.
Subsections




Next: Variabili casuali doppie discrete
Up: Variabili casuali multiple
Previous: Variabili casuali multiple
Indice
Giulio D'Agostini
2001-04-02