



Next: Variabili casuali doppie continue
Up: Vettori aleatori
Previous: Vettori aleatori
Indice
Il concetto di distribuzione di probabilità
si estende in modo naturale alle variabili multiple.
Cominciamo anche in questo caso con le variabili
discrete e, per semplicità,
con il caso bidimensionale.
L'estensione al caso generale è immediato.
La funzione di probabilità
è9.1:
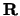 |
(9.1) |
la quale è definita non negativa e compresa fra 0 e 1.
Le possibili coppie di valori di  e
e  (o il vettore,
o n-tupla, di dimensione 2), ciascuna con il suo
grado di fiducia
(o il vettore,
o n-tupla, di dimensione 2), ciascuna con il suo
grado di fiducia 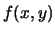 , danno luogo alla distribuzione congiunta
delle variabili.
, danno luogo alla distribuzione congiunta
delle variabili.
La condizione di normalizzazione richiede che la somma su tutte
le coppie sia pari a 1. Questo può essere scritto in diversi modi.
Anche in questo caso si definisce una funzione di ripartizione,
in perfetta analogia al caso unidimensionale:
Essa soddisfa le seguenti proprietà:
 è non decrescente, ossia
è non decrescente, ossia
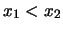 se
se
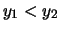 e
e 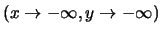 ;
;
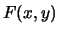 tende a 0 per
tende a 0 per
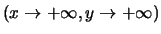 ;
;
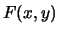 tende a 1 per
tende a 1 per
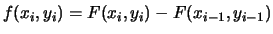 ;
;
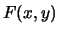 è continua a destra;
è continua a destra;
-
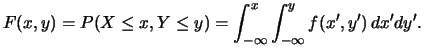 .
.
La tabella 9.1 mostra
un esempio di distribuzione doppia di variabili discrete.




Next: Variabili casuali doppie continue
Up: Vettori aleatori
Previous: Vettori aleatori
Indice
Giulio D'Agostini
2001-04-02
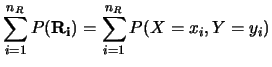 punti deve dare 1:
punti deve dare 1:
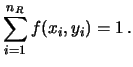
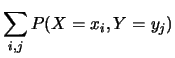
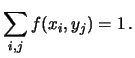
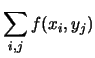 .
Se la variabile
.
Se la variabile 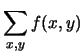
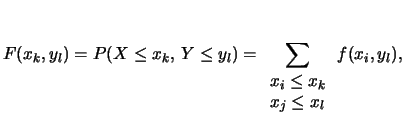
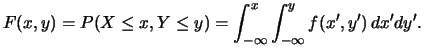 .
.