



Next: Covarianza e coefficiente di
Up: Variabili casuali multiple
Previous: Formula delle alternative e
Indice
La valutazione dei valori attese segue
in modo naturale dal caso di una sola variabile.
Questo può essere visto più
chiaramente nel caso di variabili discrete:
il valore atteso di una
funzione di variabili casuali si calcola ``facendo la somma,
estesa su tutto il campo di definizione,
del prodotto
della funzione, calcolata in ogni punto,
per la probabilità di quel punto''. Come si vede, questa definizione
non dipende dal numero di variabili casuali
(ovvero dalle dimensioni dello spazio che contiene il vettore aleatorio),
quindi nel caso
più generale:
E![$\displaystyle [g(X,Y,Z,\cdots )] = \sum_x \sum_y \sum_z \cdots \,g(x,y,z,\cdots )\, f(x,y,z,\cdots )\,.$](img2221.png) |
(9.13) |
Nel caso di variabili continue, la ``probabilità di un punto''
viene sostituita dal concetto di elemento
infinitesimo di probabilità di trovare le variabili casuali
nell'intorno di quel punto e
le sommatorie diventano integrali su tutte le variabili:
Dalla formula generale ci possiamo calcolare il valore atteso
e la varianza di ciacuna delle variabili. Prendendo, ad esempio,
la  e considerando, per semplicità, ma senza perdere in generalità,
due sole variabili continue, si tratta di calcolare
E
e considerando, per semplicità, ma senza perdere in generalità,
due sole variabili continue, si tratta di calcolare
E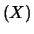 e
E
e
E![$ [(X-\mu_X)^2]$](img2225.png) . Il fatto che queste
due funzioni, di cui si è interessati al valore atteso,
dipendano soltanto
da una variabile semplifica i calcoli, in quanto, in generale
. Il fatto che queste
due funzioni, di cui si è interessati al valore atteso,
dipendano soltanto
da una variabile semplifica i calcoli, in quanto, in generale
ottenendo lo stesso risultato che si sarebbe ottenuto utilizzando
la funzione marginale della variabile di interesse.
Abbiamo quindi ricondotto il problema del calcolo di
media e di deviazione standard nel caso
molte variabili (multivariato)
a quello di una sola variabile (univariato).
Questo risultato
è ``confortante''. Difatti abbiamo già detto che per ogni evento
è possibile definire un numero arbitrario
di variabili casuali. Quando se ne considera una sola si
ignorano tutte le altre: se il valore atteso di una variabile (scelta
senza nessuna condizione restrittiva) dovesse dipendere
da tutte le altre si porrebbero problemi di definizione.




Next: Covarianza e coefficiente di
Up: Variabili casuali multiple
Previous: Formula delle alternative e
Indice
Giulio D'Agostini
2001-04-02
![$\displaystyle [g(X,Y,Z,\cdots )] = \sum_x \sum_y \sum_z \cdots \,g(x,y,z,\cdots )\, f(x,y,z,\cdots )\,.$](img2221.png)
![$\displaystyle [g(X,Y,Z,\cdots )] = \sum_x \sum_y \sum_z \cdots \,g(x,y,z,\cdots )\, f(x,y,z,\cdots )\,.$](img2221.png)
![$\displaystyle [g(X)]$](img2226.png)
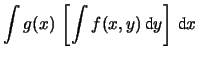 d
d![$\displaystyle \int g(x)\,
\left[ \int f(x,y)\,\mbox{d}y \right]\, \mbox{d}x$](img2228.png)