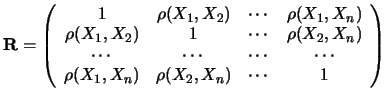Next: Esempi di variabili doppie
Up: Variabili casuali multiple
Previous: Proprietà formali di covarianza
Indice
Siamo giunti a sintetizzare l'incertezza su una coppia
di variabili con tre valori: due varianze e una covarianza, o,
equivalentemente, due deviazioni standard e un coefficiente
di correlazione.
Nel caso di  variabili (
variabili (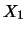 ,
, 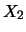 , ...
, ...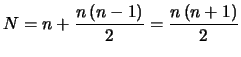 )
servono
)
servono
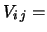 |
(9.29) |
informazioni indipendenti.
Talvolta è preferibile utilizzare una rappresentazione
compatta di queste grandezze mediante la cosidetta
matrice di correlazione, una matrice quadrata i cui
termini sono dati da
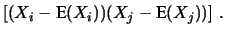 E E![$\displaystyle \left[ (X_i-\mbox{E}(X_i)) (X_j-\mbox{E}(X_j))\right]\,.$](img2300.png) |
(9.30) |
Infatti, i termini diagonali (quando  ) danno le varianze,
mentre gli altri (quando
) danno le varianze,
mentre gli altri (quando 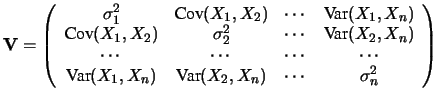 ) danno le covarianze.
In forma matriciale, abbiamo:
) danno le covarianze.
In forma matriciale, abbiamo:
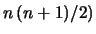 |
(9.31) |
La matrice è simmetrica, come è facile verificare,
e quindi i termini indipendenti sono esattamente
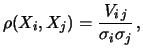 come richiesto dalla (9.29).
come richiesto dalla (9.29).
Alternativamente, a volte può essere conveniente
presentare l'incertezza dei dati mediante la matrice di correlazione,
i cui elementi sono dati da
ovvero
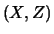 |
(9.32) |
Come si vede,
nel passaggio dalla matrice di covarianza alla matrice di correlazione
si perdono le informazioni sulle  deviazioni standard
(gli elementi della diagonale sono tutti unitari).
Quindi,
qualora si preferisca questo modo di condensare la distribuzione,
le deviazione standard devono essere fornite separatamente.
deviazioni standard
(gli elementi della diagonale sono tutti unitari).
Quindi,
qualora si preferisca questo modo di condensare la distribuzione,
le deviazione standard devono essere fornite separatamente.




Next: Esempi di variabili doppie
Up: Variabili casuali multiple
Previous: Proprietà formali di covarianza
Indice
Giulio D'Agostini
2001-04-02
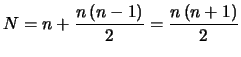 )
servono
)
servono
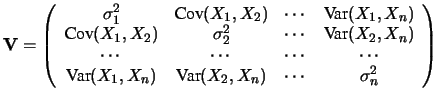 ) danno le covarianze.
In forma matriciale, abbiamo:
) danno le covarianze.
In forma matriciale, abbiamo:
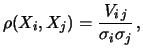 come richiesto dalla (9.29).
come richiesto dalla (9.29).