Immaginiamo di dover effettuare una serie di esperimenti che consistono
nel lancio di tre monete e nell'estrazione di una carta scelta
a caso fra due. Per ogni moneta si può verificare Testa o Croce,
mentre supponiamo che i valori delle due carte siano Asso (![]() ) e
Re (
) e
Re (![]() ). Per ogni evento possiamo costruire diverse variabili casuali,
per esempio:
). Per ogni evento possiamo costruire diverse variabili casuali,
per esempio:
Inoltre possiamo costruire a partire da queste tutte le possibili
combinazioni di variabili multiple. Ci limitiamo alle variabili doppie
![]() ,
, ![]() ,
, ![]() e
e ![]() .
Riportiamo i risultati nella tabella 9.3
.
Riportiamo i risultati nella tabella 9.3
Da questa tabella ci possiamo calcolare tutte le distribuzioni di
probabilità di interesse applicando le relazioni viste nei paragrafi
precedenti. Cominciamo con le variabili ![]()
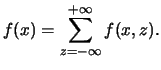 |
|
| (0,0) | 2/16 |
| (1,0) | 6/16 |
| (2,0) | 2/16 |
| (2,1) | 4/16 |
| (3,2) | 2/16 |
Da questa possiamo ricavare le distribuzioni marginali di ![]() e
e ![]() .
Per esempio, per ottenere
.
Per esempio, per ottenere ![]() bisogna , per ogni valore
di
bisogna , per ogni valore
di ![]() , ``integrare'' su tutti i valori di
, ``integrare'' su tutti i valori di ![]() :
:
| 0 |
|
| 1 |
|
| 2 |
|
| 3 |
|
| 0 |
|
| 1 |
|
| 2 |
|
Come si vede dalla tabella, la distribuzione
marginale di una certa variabile
calcolata dalla formula
è esattamente quella che si otterrebbe
esaminando la tabella ove sono riportati gli
eventi elementari e ignorando tutte le altre variabili.
Dalla distribuzione di probabilità di ![]() ci possiamo
costruire anche le distribuzioni condizionali
ci possiamo
costruire anche le distribuzioni condizionali
![]() . Come detto, di
queste distribuzioni ne esiste una per ogni valore di
. Come detto, di
queste distribuzioni ne esiste una per ogni valore di ![]() . È interessante,
in questo semplice caso, confrontare il risultato che si ottiene contando
il numero di casi favorevoli e il numero di casi possibili con quello
che si otterrebbe applicando le formule delle variabili condizionali
viste sopra:
. È interessante,
in questo semplice caso, confrontare il risultato che si ottiene contando
il numero di casi favorevoli e il numero di casi possibili con quello
che si otterrebbe applicando le formule delle variabili condizionali
viste sopra:
|
|
||
| 0 |
|
|
| 1 |
|
|
| 2 |
|
|
|
|
||
| 2 | 1 |
|
|
|
||
| 3 | 1 |
|
Queste sono le altre distribuzioni di variabili doppie ottenibili dalla tabella degli eventi elementari9.4:
| (0,2) | 2/16 |
| (1,0) | 2/16 |
| (1,1) | 4/16 |
| (2,0) | 6/16 |
| (3,0) | 2/16 |
| (0,0) | 1/16 |
| (0,1) | 3/16 |
| (0,2) | 3/16 |
| (0,3) | 1/16 |
| (1,0) | 1/16 |
| (1,1) | 3/16 |
| (1,2) | 3/16 |
| (1,3) | 1/16 |
| (0,0) | 5/16 |
| (0,1) | 2/16 |
| (0,2) | 1/16 |
| (1,0) | 5/16 |
| (1,1) | 2/16 |
| (1,2) | 1/16 |
La distribuzione marginale di ![]() è
è
| 0 | 1/2 |
| 1 | 1/2 |
Come ultimo esempio ci costruiamo la distribuzione condizionale di
![]() sotto la condizione
sotto la condizione ![]() .
.
|
|
|
|
| 0 | 1/8 |
|
| 1 | 3/8 |
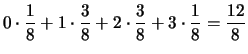 |
| 2 | 3/8 |
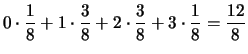 |
| 3 | 1/8 |
|
Da quest'ultima tabella si vede che che la distribuzione
di ![]() sotto la condizione
sotto la condizione ![]() è uguale a quella marginale di
è uguale a quella marginale di ![]() , contrariamente a quanto accadeva
quando la variabile condizionante era
, contrariamente a quanto accadeva
quando la variabile condizionante era ![]() . Questo corrisponde al fatto che,
mentre lo stato di conoscenza del numero di
teste consecutive condiziona il grado di fiducia del
numero di teste, questo non è influenzato dal sapere se si
è verificato un Asso o un Re.
. Questo corrisponde al fatto che,
mentre lo stato di conoscenza del numero di
teste consecutive condiziona il grado di fiducia del
numero di teste, questo non è influenzato dal sapere se si
è verificato un Asso o un Re.
Calcoliamo ora valori attesi di ciascuna variabile:
| E |
|||
E |
|||
| E |
|||
E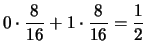 |
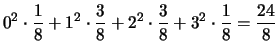 |
| E |
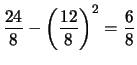 |
||
| Var |
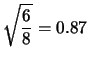 |
||
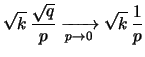 |
|||
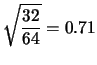 |
|||
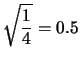 |
E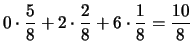 |
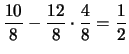 |
||
Cov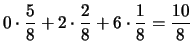 |
(9.33) | ||
| (9.34) |
E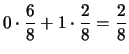 |
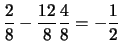 |
||
Cov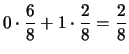 |
(9.35) | ||
| (9.36) |
E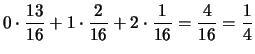 |
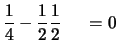 |
||
Cov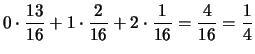 |
(9.37) | ||
| (9.38) |