



Next: Distribuzione uniforme in un
Up: Esempi di distribuzione bidimensionale
Previous: Esempi di distribuzione bidimensionale
Indice
Come primo e semplice esempio di distribuzione multipla
di variabili continue consideriamo due variabili  e
e  negli intervalli
negli intervalli
![$ [x_1, x_2]$](img2373.png) e
e
![$ [y_1, y_2]$](img2374.png) e tali
che la loro densità di probabilità congiunta
e tali
che la loro densità di probabilità congiunta
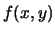 sia
costante nella porzione di piano definita da tali limiti.
Per semplificare i conti, ma senza perdere in generalità,
facciamo coincidere gli estremi inferiori
sia
costante nella porzione di piano definita da tali limiti.
Per semplificare i conti, ma senza perdere in generalità,
facciamo coincidere gli estremi inferiori 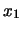 e
e 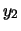 con
l'origine degli assi, e chiamiamo
con
l'origine degli assi, e chiamiamo  e
e 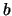 le lunghezze
dei due segmenti (vedi figura 9.3).
le lunghezze
dei due segmenti (vedi figura 9.3).
Figura:
Distribuzione bidimensionale uniforme
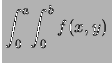 |
La condizione di normalizzazione permette di ricavare il
valore della costante:
da cui segue
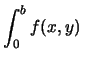 |
(9.40) |
Possiamo quindi calcolare le distribuzioni marginali delle due
variabili:
Come ovvio, la densità è uniforme in ciascuna delle due
distribuzioni. Le medie e le varianze valgono quindi:
E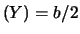 ;
E
;
E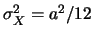 ;
;
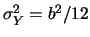 ;
;
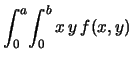 .
.
Per il calcolo della covarianza serve il valore atteso del prodotto:
da cui
e quindi
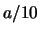 . In effetti, anche se si venisse a
sapere che
. In effetti, anche se si venisse a
sapere che  vale
vale 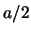 ,
, 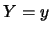 o
o  , questa informazione non cambia
le nostre aspettative sui possibili valori di
, questa informazione non cambia
le nostre aspettative sui possibili valori di  .
.
Il calcolo della densità di probabilità di  ,
condizionata dall'occorrenza di un valore di
,
condizionata dall'occorrenza di un valore di 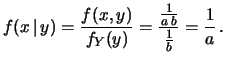 ,
è altresì semplice:
,
è altresì semplice:
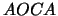 |
(9.45) |
Essa è identica alla densità marginale e quindi  e
e  sono indipendenti.
sono indipendenti.




Next: Distribuzione uniforme in un
Up: Esempi di distribuzione bidimensionale
Previous: Esempi di distribuzione bidimensionale
Indice
Giulio D'Agostini
2001-04-02
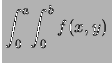
![$ [y_1, y_2]$](img2374.png) e tali
che la loro densità di probabilità congiunta
e tali
che la loro densità di probabilità congiunta
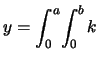 d
d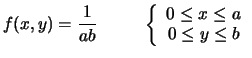
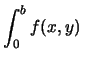
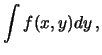
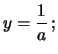 d
d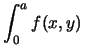
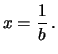 d
d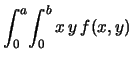 .
.
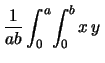 d
d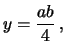 d
d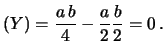 E
E![]() ,
condizionata dall'occorrenza di un valore di
,
condizionata dall'occorrenza di un valore di 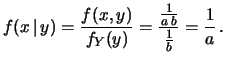 ,
è altresì semplice:
,
è altresì semplice: