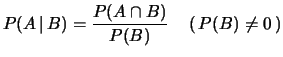Next: pzd100 Distribuzione multinomiale
Up: Esempi di distribuzione bidimensionale
Previous: Distribuzione uniforme in un
Indice
Se le variabili casuali possono assumere valori,
sempre in modo uniforme, all'interno del triangolo 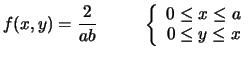 di figura 9.3, la funzione densità di probabilità
congiunta è data da
di figura 9.3, la funzione densità di probabilità
congiunta è data da
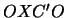 |
(9.46) |
È possibile ottenere le distribuzioni marginali e condizionate
senza fare alcun conto:
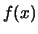 è ottenuta integrando
è ottenuta integrando 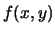 lungo
lungo 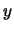 e quindi è proporzionale
all'altezza del triangolo rettangolo
e quindi è proporzionale
all'altezza del triangolo rettangolo
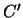 , ove
, ove 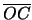 indica il punto lungo la diagonale
indica il punto lungo la diagonale
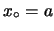 in corrispondenza di
in corrispondenza di  .
la distribuzione marginale di
.
la distribuzione marginale di  è quindi una triangolare
asimmetrica (vedi paragrafo 8.4) avente
è quindi una triangolare
asimmetrica (vedi paragrafo 8.4) avente
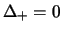 ,
,
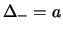 e
e
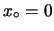 ;
;
- per simmetria
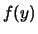 è data da una triangolare avente
è data da una triangolare avente
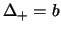 ,
,
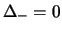 e
e
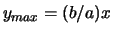 ;
;
- fissando
 la distribuzione di
la distribuzione di  è una uniforme
fra 0 e
è una uniforme
fra 0 e
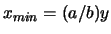 .;
.;
- analogamente, fissando
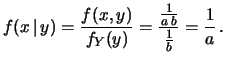 la distribuzione di
la distribuzione di  è uniforme fra
è uniforme fra
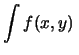 e
e  .
.
Come esercizio facciamo i conti:
Si ricordi che le nelle funzioni densità di probabilità
condizionate il condizionante
ha il ruolo di parametro. A differenza del caso precedente,
le funzioni le condizionate e le marginali sono diverse: sapere
che  vale 0,
vale 0, 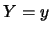 o
o  cambia lo stato di incertezza su
cambia lo stato di incertezza su
 . Ad esempio, la previsione (
. Ad esempio, la previsione ( incertezza standard) vale nei tre
casi:
incertezza standard) vale nei tre
casi: 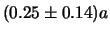 (certezza!),
(certezza!),
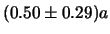 e
e
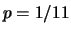 .
.




Next: pzd100 Distribuzione multinomiale
Up: Esempi di distribuzione bidimensionale
Previous: Distribuzione uniforme in un
Indice
Giulio D'Agostini
2001-04-02
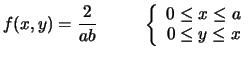 di figura 9.3, la funzione densità di probabilità
congiunta è data da
di figura 9.3, la funzione densità di probabilità
congiunta è data da
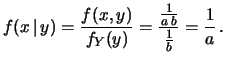 la distribuzione di
la distribuzione di 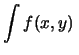 e
e 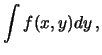
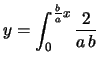 d
d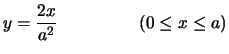 d
d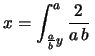
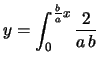 d
d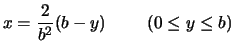 d
d