



Next: pzd100Distribuzione normale bivariata
Up: Variabili casuali multiple
Previous: Distribuzione uniforme in un
Indice
Dopo aver introdotto i concetti di base delle distribuzioni
multivariate e alcuni esempi elementari, mostriamo ora una
una distribuzione di variabile discreta che descrive
i possibili istogrammi che possono essere osservati effettuando un certo
esperimento.
Questo argomento era già stato introdotto nel paragrafo
7.14. In tale occasione ci eravamo
interessati soltanto della previsione della distribuzione statistica,
ma era stato tralasciato il problema di calcolare la probabilità
di ciascuna delle possibili configurazioni.
Cominciamo con un esempio numerico. Immaginiamo di ripetere 20 volte un
certo esperimento, in ciascuno crediamo che possa uscire, con uguale
probabilità, un numero
intero 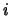 compreso fra 0 e 10. Indichiamo con
compreso fra 0 e 10. Indichiamo con 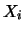 il numero
di occorrenze dell'esito
il numero
di occorrenze dell'esito 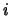 -mo. Riassumiamo le cose che già
sappiamo fare:
-mo. Riassumiamo le cose che già
sappiamo fare:
- ciascuna variabile
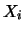 è distribuita secondo una binomiale di
è distribuita secondo una binomiale di
 e
e 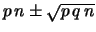 ;
;
- prevediamo una distribuzione statistica con
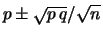 occorrenze per ciascun esito; (*** att ***)
occorrenze per ciascun esito; (*** att ***)
- prevediamo che le frequenze relative siano
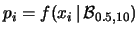 .
.
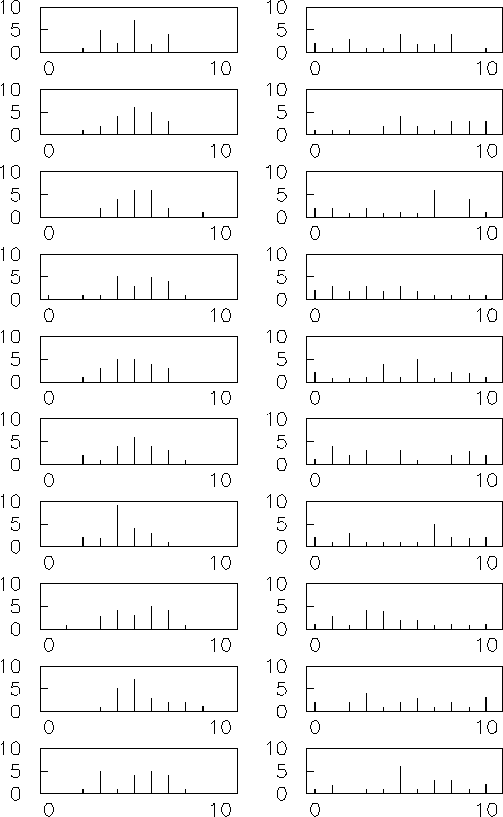
Interessiamoci ora delle possibili configurazioni di occorrenze
che è possibile osservare. La figura
9.4 (parte a destra) ne mostra
qualcuna (istogramma ottenuto da simulazione al calcolatore).
Figura:
Esempi di eventi multinomiali generati casualmente.
Tutte le distribuzioni hanno il parametro  pari a 20,
pari a 20,
 ,
, 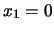 e
e 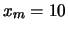 . Negli
istogrammi a destra
. Negli
istogrammi a destra 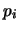 è costante e pari
è costante e pari 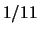 , mentre
in quelli a sinistra vale invece
, mentre
in quelli a sinistra vale invece
 .
.
 |
Cominciamo con dei casi particolari e poi
passeremo alla trattazione generale.
- Può capitare 20 volte di seguito lo stesso valore di
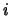 , ad esempio
, ad esempio
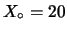 , dando luogo a
, dando luogo a
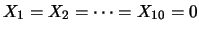 e
e
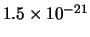 , con
probabilità
, con
probabilità
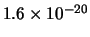 per ciascuna possibilità.
(La probabilità che si verifichi uno qualsiasi di
questo tipo di eventi
è
per ciascuna possibilità.
(La probabilità che si verifichi uno qualsiasi di
questo tipo di eventi
è
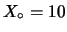 .)
.)
- Può capitare che esca la metà delle volte un valore, l'altra metà
un altro e nessuna volta gli altri 9. Concentriamoci su
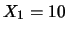 ,
,
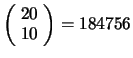 e gli altri zero. Questi valori possono essere ottenuti
da
e gli altri zero. Questi valori possono essere ottenuti
da
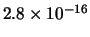 possibili sequenze,
ciascuna avente probabilità
possibili sequenze,
ciascuna avente probabilità
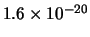 . Ne seque che
la probabilità dell'evento
. Ne seque che
la probabilità dell'evento
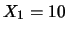 ,
, 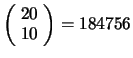 è uguale a
è uguale a
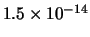 . (Per calcolare la probabilità di osservare
una qualsiasi equipartizione dei 20 successi in due classi
bisogna considerare il numero combinazioni di 11 esiti presi 2 a 2,
pari a 55, ottenendo
. (Per calcolare la probabilità di osservare
una qualsiasi equipartizione dei 20 successi in due classi
bisogna considerare il numero combinazioni di 11 esiti presi 2 a 2,
pari a 55, ottenendo
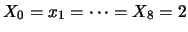 .)
.)
- Consideriamo ora un caso in cui i risultati sono ``più equilibrati'',
ad esempio i primi 9 esiti che si verificano 2 volte e gli ultimi due
una sola volta:
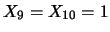 ;
;
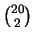 . Questo sembra
essere, intuitivamente, un risultato molto più probabile
dei due precedenti. Calcoliamo il numero di sequenze (tutte di
probabilità
. Questo sembra
essere, intuitivamente, un risultato molto più probabile
dei due precedenti. Calcoliamo il numero di sequenze (tutte di
probabilità
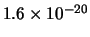 ):
):
- ci sono
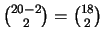 combinazioni che danno
combinazioni che danno 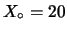 ;
;
- per ciascuna di esse ce ne sono
 che danno
che danno 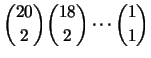 e così via;
e così via;
- otteniamo un totale di
combinazioni, ovvero:
Questa configurazione ha quindi una probabilità di
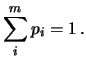 ,
enormemente più alta delle altre, anche se di per sé ancora
molto piccola. Se poi consideriamo che ci sono 55 configurazioni
distinte
in cui 9 esiti possono uscire 2 volte e gli altri 1 volta,
otteniamo una probabilità di circa lo 0.4 per mille di osservare
una qualsiasi di queste configurazioni ``equilibrate''.
,
enormemente più alta delle altre, anche se di per sé ancora
molto piccola. Se poi consideriamo che ci sono 55 configurazioni
distinte
in cui 9 esiti possono uscire 2 volte e gli altri 1 volta,
otteniamo una probabilità di circa lo 0.4 per mille di osservare
una qualsiasi di queste configurazioni ``equilibrate''.
Passiamo ora al caso generale di
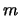 possibili modalitè per l'esito
di ciascuna prova e sia
possibili modalitè per l'esito
di ciascuna prova e sia 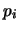 la probabilità
che assegniamo a ciscuna modalità. Naturalmente
deva valere la condizione
la probabilità
che assegniamo a ciscuna modalità. Naturalmente
deva valere la condizione
Dovendo effettuare  prove nelle stesse condizioni possiamo osservare
prove nelle stesse condizioni possiamo osservare
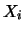 volte ciascun esito, con
Le
volte ciascun esito, con
Le  prove possono dar luogo a
prove possono dar luogo a 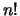 sequenze possibili, in genere
non tutte equiprobabili (a meno che le
sequenze possibili, in genere
non tutte equiprobabili (a meno che le 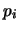 siano tutte uguali).
Ciascuna sequenza che produce la configurazione
di variabili casuali
siano tutte uguali).
Ciascuna sequenza che produce la configurazione
di variabili casuali 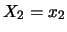 ,
, 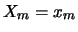 , ...
, ...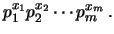 ha probabilità
ha probabilità
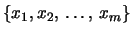 |
(9.47) |
Il numero delle sequenze che produce la stessa configurazione
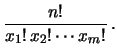 è dato dal coefficiente multinomiale
è dato dal coefficiente multinomiale
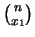 |
(9.48) |
Infatti, si hanno
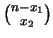 combinazioni per la prima modalità; per ciascuna di esse
ce ne sono
combinazioni per la prima modalità; per ciascuna di esse
ce ne sono
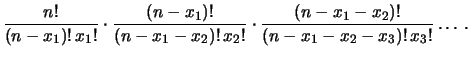 la seconda, e così via. Quindi il numero di combinazioni è
Semplificando otteniamo la (9.50). Moltiplicando
la probabilità (9.49) della sequenza per
il numero di sequanze abbiamo finalmente la
distribuzione multinomiale
la seconda, e così via. Quindi il numero di combinazioni è
Semplificando otteniamo la (9.50). Moltiplicando
la probabilità (9.49) della sequenza per
il numero di sequanze abbiamo finalmente la
distribuzione multinomiale
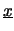 |
(9.49) |
dove con
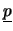 è stato indicato l'insieme dei valori
è stato indicato l'insieme dei valori
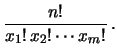 e con
e con
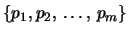 l'insieme delle probabilità
l'insieme delle probabilità
 .
Quando
.
Quando 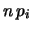 si riottiene la binomiale.
si riottiene la binomiale.
Il calcolo del valore atteso e della varianza di ciascuna variabile
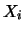 è immediato, in quanto è sufficiente pensare la
distribuzione marginale di ogni variabile
pari ad una distribuzione binomiale
di parametro
è immediato, in quanto è sufficiente pensare la
distribuzione marginale di ogni variabile
pari ad una distribuzione binomiale
di parametro 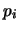 . Ne segue
. Ne segue
Per quanto riguarda covarianza e coefficiente
di correlazione, invece del conto esatto utilizziamo un
metodo euristico (più importante del conto esatto
per l'impostazione di questo corso).
Riprendiamo la funzione di probabilità della distribuzione
binomiale
ed esplicitiamo il fatto ci troviamo di fronte
a due classi di eventi
(favorevoli e sfavorevoli) scrivendo
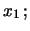 |
(9.52) |
dove è stata operata la seguente trasformazione di simboli:
Il fatto che adesso
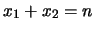 dipenda apparentemente da due
variabili non è in contraddizione con il fatto che la formula
originale delle binomiale fosse funzione di una sola variabile.
Infatti
dipenda apparentemente da due
variabili non è in contraddizione con il fatto che la formula
originale delle binomiale fosse funzione di una sola variabile.
Infatti 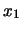 e
e 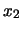 sono linermente (anti-)correlate in quanto
devono soddisfare la condizione
sono linermente (anti-)correlate in quanto
devono soddisfare la condizione 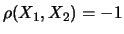 .
Quindi
.
Quindi
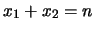 dipende in realtà soltanto da una variabile e
il coefficiente di correlazione
fra le due variabili vale
dipende in realtà soltanto da una variabile e
il coefficiente di correlazione
fra le due variabili vale
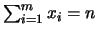 , come è
intuitivo pensare e come risulta dalla (9.25)
, come è
intuitivo pensare e come risulta dalla (9.25)
Anche nel caso generale della multinomiale le
variabili 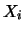 sono fra loro correlate,
in quanto vale la relazione
sono fra loro correlate,
in quanto vale la relazione
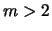 . Ma il grado di
correlazione è, per
. Ma il grado di
correlazione è, per 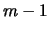 ,
minore che nella binomiale.
Infatti, mentre nel caso
,
minore che nella binomiale.
Infatti, mentre nel caso 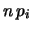 il non verificarsi di un evento nella classe 1
implica il suo verificarsi nella classe 2, nel caso di molte classi si può
al più affermare che esso si sia verificato in una delle restanti
il non verificarsi di un evento nella classe 1
implica il suo verificarsi nella classe 2, nel caso di molte classi si può
al più affermare che esso si sia verificato in una delle restanti
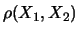 classi, ciascuna con probabilità proporzionale a
classi, ciascuna con probabilità proporzionale a 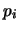 . Quindi il
grado di correlazione diminuisce in valore assoluto (``si diluisce'')
al crescere del numero di classi e, per
. Quindi il
grado di correlazione diminuisce in valore assoluto (``si diluisce'')
al crescere del numero di classi e, per 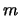 abbastanza grande,
la multinomiale può essere essere vista come la probabilità congiunta
di tante binomiali indipendenti.
abbastanza grande,
la multinomiale può essere essere vista come la probabilità congiunta
di tante binomiali indipendenti.
Abbiamo detto che nel caso binomiale
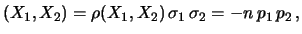 vale -1. Ne
segue che
vale -1. Ne
segue che
Cov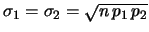 |
(9.53) |
in quanto
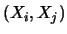 .
In effetti si può verificare che la (9.55)
è valida anche nel caso generale. Si ottiene quindi:
.
In effetti si può verificare che la (9.55)
è valida anche nel caso generale. Si ottiene quindi:
Come previsto qualitativamente, la correlazione è trascurabile
se le probabilità delle due
classi sono abbastanza piccole9.5.
L'importanza della distribuzione multinomiale
risiede nel fatto che essa
descrive il numero di eventi di un istogramma o di un
diagramma a barre, indipendentemente dalla distribuzione
di probabilità che segue
la variabile casuale associata alla grandezza di cui si
costruisce l'istogramma o il diagramma a barre in questione.
In Fig 9.4 sono riportati degli
esempi di eventi
casuali generati secondo due distribuzioni multinomiali
di  ,
in un caso (grafici a destra) con
,
in un caso (grafici a destra) con 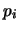 tutte uguali e
nell'altro con
tutte uguali e
nell'altro con 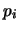 generato secondo una binomiale:
generato secondo una binomiale:
 . In questo caso
il numero di eventi per ciascun
. In questo caso
il numero di eventi per ciascun 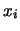 è distribuito
secondo una binomiale di parametri
è distribuito
secondo una binomiale di parametri 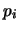 ed
ed  , e quindi
ha un valore medio
, e quindi
ha un valore medio 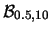 . Quindi le realizzazioni della
multinomiale dell'esempio fluttuano intorno ad un andamento medio
che ha la stessa forma della distribuzione di
. Quindi le realizzazioni della
multinomiale dell'esempio fluttuano intorno ad un andamento medio
che ha la stessa forma della distribuzione di 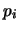 ,
riscalato (``normalizzato'') di un fattore 20.
Si confrontino questi grafici con quello della distribuzione
,
riscalato (``normalizzato'') di un fattore 20.
Si confrontino questi grafici con quello della distribuzione
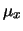 di Fig. 7.1.
di Fig. 7.1.




Next: pzd100Distribuzione normale bivariata
Up: Variabili casuali multiple
Previous: Distribuzione uniforme in un
Indice
Giulio D'Agostini
2001-04-02
![]() compreso fra 0 e 10. Indichiamo con
compreso fra 0 e 10. Indichiamo con ![]() il numero
di occorrenze dell'esito
il numero
di occorrenze dell'esito ![]() -mo. Riassumiamo le cose che già
sappiamo fare:
-mo. Riassumiamo le cose che già
sappiamo fare:
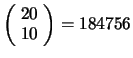 e gli altri zero. Questi valori possono essere ottenuti
da
e gli altri zero. Questi valori possono essere ottenuti
da
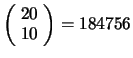 è uguale a
è uguale a
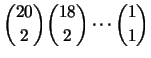 e così via;
e così via;
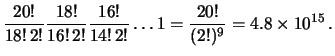
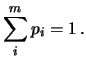 ,
enormemente più alta delle altre, anche se di per sé ancora
molto piccola. Se poi consideriamo che ci sono 55 configurazioni
distinte
in cui 9 esiti possono uscire 2 volte e gli altri 1 volta,
otteniamo una probabilità di circa lo 0.4 per mille di osservare
una qualsiasi di queste configurazioni ``equilibrate''.
,
enormemente più alta delle altre, anche se di per sé ancora
molto piccola. Se poi consideriamo che ci sono 55 configurazioni
distinte
in cui 9 esiti possono uscire 2 volte e gli altri 1 volta,
otteniamo una probabilità di circa lo 0.4 per mille di osservare
una qualsiasi di queste configurazioni ``equilibrate''.
![]() possibili modalitè per l'esito
di ciascuna prova e sia
possibili modalitè per l'esito
di ciascuna prova e sia ![]() la probabilità
che assegniamo a ciscuna modalità. Naturalmente
deva valere la condizione
la probabilità
che assegniamo a ciscuna modalità. Naturalmente
deva valere la condizione
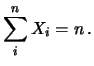
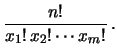 è dato dal coefficiente multinomiale
è dato dal coefficiente multinomiale
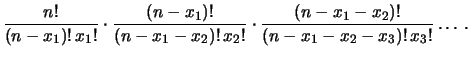 la seconda, e così via. Quindi il numero di combinazioni è
la seconda, e così via. Quindi il numero di combinazioni è
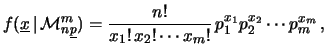
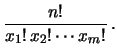 e con
e con
![]() è immediato, in quanto è sufficiente pensare la
distribuzione marginale di ogni variabile
pari ad una distribuzione binomiale
di parametro
è immediato, in quanto è sufficiente pensare la
distribuzione marginale di ogni variabile
pari ad una distribuzione binomiale
di parametro ![]() . Ne segue
. Ne segue
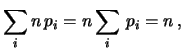
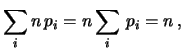
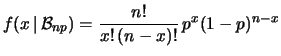
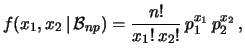
![]() sono fra loro correlate,
in quanto vale la relazione
sono fra loro correlate,
in quanto vale la relazione
![]() . Ma il grado di
correlazione è, per
. Ma il grado di
correlazione è, per ![]() ,
minore che nella binomiale.
Infatti, mentre nel caso
,
minore che nella binomiale.
Infatti, mentre nel caso ![]() il non verificarsi di un evento nella classe 1
implica il suo verificarsi nella classe 2, nel caso di molte classi si può
al più affermare che esso si sia verificato in una delle restanti
il non verificarsi di un evento nella classe 1
implica il suo verificarsi nella classe 2, nel caso di molte classi si può
al più affermare che esso si sia verificato in una delle restanti
![]() classi, ciascuna con probabilità proporzionale a
classi, ciascuna con probabilità proporzionale a ![]() . Quindi il
grado di correlazione diminuisce in valore assoluto (``si diluisce'')
al crescere del numero di classi e, per
. Quindi il
grado di correlazione diminuisce in valore assoluto (``si diluisce'')
al crescere del numero di classi e, per ![]() abbastanza grande,
la multinomiale può essere essere vista come la probabilità congiunta
di tante binomiali indipendenti.
abbastanza grande,
la multinomiale può essere essere vista come la probabilità congiunta
di tante binomiali indipendenti.
![]() vale -1. Ne
segue che
vale -1. Ne
segue che
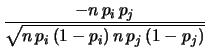
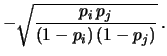
![]() ,
in un caso (grafici a destra) con
,
in un caso (grafici a destra) con ![]() tutte uguali e
nell'altro con
tutte uguali e
nell'altro con ![]() generato secondo una binomiale:
generato secondo una binomiale:
 . In questo caso
il numero di eventi per ciascun
. In questo caso
il numero di eventi per ciascun ![]() è distribuito
secondo una binomiale di parametri
è distribuito
secondo una binomiale di parametri ![]() ed
ed ![]() , e quindi
ha un valore medio
, e quindi
ha un valore medio ![]() . Quindi le realizzazioni della
multinomiale dell'esempio fluttuano intorno ad un andamento medio
che ha la stessa forma della distribuzione di
. Quindi le realizzazioni della
multinomiale dell'esempio fluttuano intorno ad un andamento medio
che ha la stessa forma della distribuzione di ![]() ,
riscalato (``normalizzato'') di un fattore 20.
Si confrontino questi grafici con quello della distribuzione
,
riscalato (``normalizzato'') di un fattore 20.
Si confrontino questi grafici con quello della distribuzione
![]() di Fig. 7.1.
di Fig. 7.1.