



Next: pzd100 Caso generale di
Up: Variabili casuali multiple
Previous: pzd100 Distribuzione multinomiale
Indice
pzd100Distribuzione normale bivariata
Una funzione di distribuzione di variabili multiple particolarmente
importante per le applicazione è quella in cui tutte
le distribuzioni marginali sono normali. Consideriamo per ora
il caso di due
sole variabili, rimandando nei prossimi paragrafi il caso generale.
La situazione più semplice si verifica se le due
variabili casuali sono indipendenti.
Nel tale caso la densità congiunta
è data semplicemente dal prodotto delle densità
marginali. Chiamando  e
e  le variabili e
le variabili e
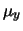 ,
, 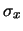 ,
, 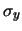 e
e 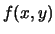 i parametri delle gaussiane
otteniamo
i parametri delle gaussiane
otteniamo
Il caso in cui le variabili sono correlate è decisamente più complicato.
Rinunciamo ad una trattazione rigorosa e cerchiamo di capire
la forma della distribuzione ragionando sulla dipendenza della
densità condizionata
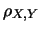 dai parametri delle gaussiane e dal coefficiente di
correlazione
dai parametri delle gaussiane e dal coefficiente di
correlazione 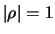 (nel seguito indichiamo
(nel seguito indichiamo
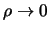 semplicemente come
semplicemente come 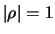 ).
).
- Nel limite
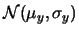 si deve riottenere la distribuzione
marginale
si deve riottenere la distribuzione
marginale
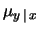 .
.
- Se
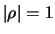 è diverso da zero la
è diverso da zero la
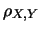 è distribuita
intorno ad un valore medio diverso da
è distribuita
intorno ad un valore medio diverso da 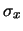 e avente una diversa varianza. In particolare, chiamando
e avente una diversa varianza. In particolare, chiamando
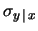 e
e
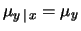 i parametri della distribuzione
condizionata:
i parametri della distribuzione
condizionata:
-
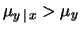 se
se 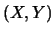
-
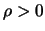 se
se 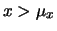 e
e 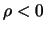 ,
oppure se
,
oppure se 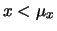 e
e 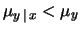 ;
;
-
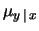 se
se 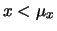 e
e 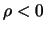 ,
oppure se
,
oppure se 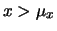 e
e 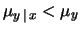 ;
;
- l'effetto di
spostamento da
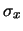 deve dipendere, oltre che dal
segno, anche dall'entità della correlazione;
deve dipendere, oltre che dal
segno, anche dall'entità della correlazione;
- esso
deve dipendere dai rapporti fra le
larghezze delle
due gaussiane:
se, ad esempio,
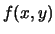 è maggiore di
è maggiore di 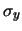 ,
una piccola deviazione di
,
una piccola deviazione di  da
da 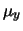 produrrà una grande
deviazione di
produrrà una grande
deviazione di
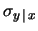 da
da 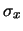 .
.
- anche la deviazione standard della distribuzione condizionata
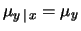 deve
dipendere da
deve
dipendere da 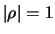 , nel senso che si deve riottenere
, nel senso che si deve riottenere 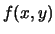 per variabili scorrelate, mentre essa si deve annullare nel caso di
correlazione lineare (
per variabili scorrelate, mentre essa si deve annullare nel caso di
correlazione lineare ( ). In quest'ultimo caso infatti
ogni valore di
). In quest'ultimo caso infatti
ogni valore di  determina univocamente un valore di
determina univocamente un valore di  .
Inoltre questo effetto di strizzamento della distribuzione non
deve dipendere dal segno di
.
Inoltre questo effetto di strizzamento della distribuzione non
deve dipendere dal segno di 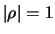 .
La forma esatta della dipendenza funzionale è meno intuitiva, ma
il risultato esatto è in accordo con le aspettative.
.
La forma esatta della dipendenza funzionale è meno intuitiva, ma
il risultato esatto è in accordo con le aspettative.
Queste semplici considerazioni
sono in accordo con i risultati esatti dati dalle
seguenti relazioni:
- Assumiamo inoltre che anche la distribuzione condizionata
sia normale (fatta eccezione del caso degenere quando
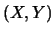 e
e
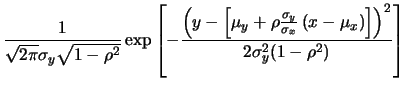 ).
).
Mettendo insieme i vari ingredienti otteniamo:
Utilizzando la formula della densità condizionata si giunge finalmente
alla distribuzione congiunta 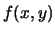 :
:
dove con 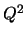 si è indicata la forma quadratica che
compare nell'argomento dell'esponenziale,
che dopo le opportune
semplificazioni, ha la seguente forma:
si è indicata la forma quadratica che
compare nell'argomento dell'esponenziale,
che dopo le opportune
semplificazioni, ha la seguente forma:
![$\displaystyle Q^2=\frac{1}{1-\rho^2} \left[ \frac{(x-\mu_x)^2}{\sigma_x^2} - 2\...
...{(x-\mu_x)(y-\mu_y)}{\sigma_x\sigma_y} + \frac{(y-\mu_y)^2}{\sigma_y^2} \right]$](img2517.png) |
(9.58) |
È facile convincersi che, per definizione, 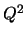 è una quantità
non negativa, la quale si annulla nel solo punto
è una quantità
non negativa, la quale si annulla nel solo punto 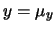 e
e 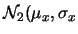 ,
dove ha chiaramente un minimo.
,
dove ha chiaramente un minimo.
La probabilità congiunta 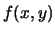 descritta dalla (9.59)
è nota come la normale bivariata,
o binormale e la possiamo indicare con
descritta dalla (9.59)
è nota come la normale bivariata,
o binormale e la possiamo indicare con
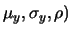 ,
,
 .
.
Si può verificare facilmente che, nel caso
di correlazione nulla, si riottiene la densità congiunta
ottenuta precedentemente dal prodotto delle due gaussiane.
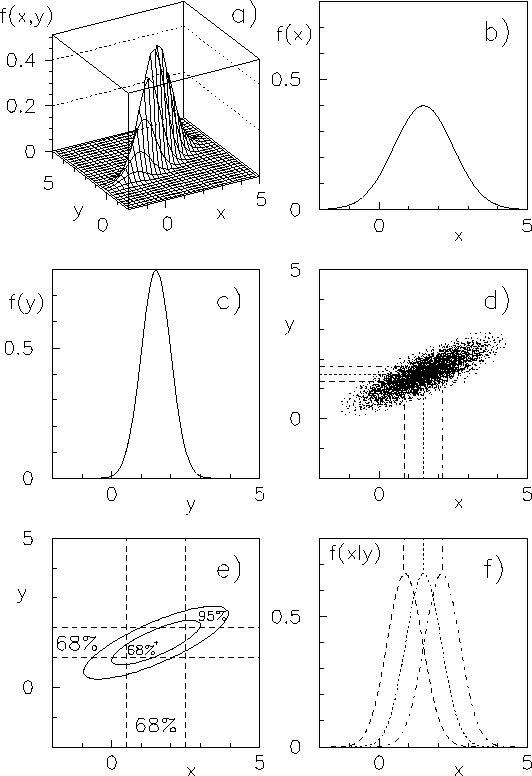
Figura:
Esempio di distribuzione normale bivariata.
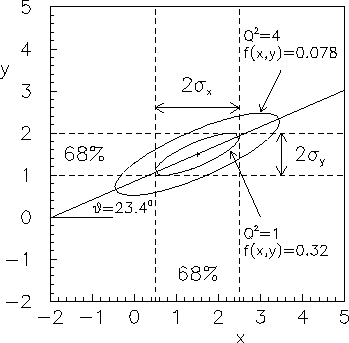 |
Figura:
Distribuzione normale
bivariata: ellissi di equidensità e parametri delle distribuzioni
marginali. I valori numerici di 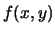 e di
e di 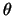 dipendono
dai parametri dell'esempio.
dipendono
dai parametri dell'esempio.
 |
Terminiamo elencando alcune sue proprietà, alcune delle
quali già incontrate, e facendo riferimento alle
Figg. 9.5 e 9.6.
- Rappresentata nello spazio, essa
ha una tipica forma a campana, più
o meno schiacciata e più o meno inclinata, a seconda dei
valori dei parametri.
- Il valore massimo di
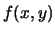 è situato in corrispondenza di
è situato in corrispondenza di 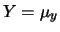 e
e 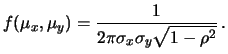 e vale
e vale
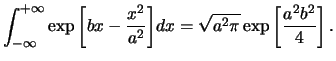 |
(9.59) |
Esso dipende, oltre che dall'inverso delle deviazioni standard,
anche dal coeffiente di correlazione.
- La distribuzione marginale di ciascuna delle variabili
è normale come si può verificare integrando9.6 la ( 9.59).
- I valori attesi delle variabili
 e
e  sono
sono 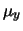 e
e 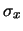 e le loro deviazioni standard
e le loro deviazioni standard
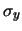 e
e 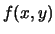 .
.
- La covarianza fra le variabili vale
Cov
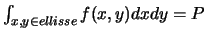 .
.
- I valori di
 e
e  per i quali la densità di probabilità
è costante sono quelli per i quali è costante
per i quali la densità di probabilità
è costante sono quelli per i quali è costante 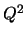 .
Si riconosce facilmente come tali punti, per una dato
valore di
.
Si riconosce facilmente come tali punti, per una dato
valore di 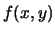 , definiscono un'ellisse
nel piano
, definiscono un'ellisse
nel piano 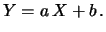 , chiamata ellisse di equidensità;
di particolare interesse sono due famiglie di ellissi:
, chiamata ellisse di equidensità;
di particolare interesse sono due famiglie di ellissi:
- ellissi esattamente contenute entro rettangoli
di lati
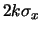 e
e
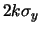 centrati intorno
a
centrati intorno
a 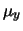 e
e 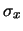 (Fig 9.6);
(Fig 9.6);
- ellissi tali da avere un certo livello
probabilità
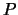 che entrambe
le variabili cadano all'interno di esse (Fig 9.5.E).
che entrambe
le variabili cadano all'interno di esse (Fig 9.5.E).
Le prime ellissi possono essere ricavate direttamente da considerazioni
geometriche, mentre per le altre è necessario calcolare
l'integrale
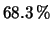 . È interessante sapere
che queste ultime ellissi dipendono da
. È interessante sapere
che queste ultime ellissi dipendono da 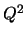 in modo indipendente dagli
altri parametri, mentre invece i valori di
in modo indipendente dagli
altri parametri, mentre invece i valori di 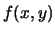 sono
irrilevati in quanto dipendono da
sono
irrilevati in quanto dipendono da 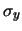 ,
, 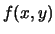 e
e 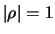 .
.
Tabella:
Valori di 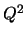 per calcolare le ellissi
contenute esattamente entro i rettangoli di
ampiezza
per calcolare le ellissi
contenute esattamente entro i rettangoli di
ampiezza
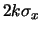 e
e
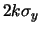 intorno ai valori medi.
intorno ai valori medi.
| k |
1 (1.65) |
2 (1.96) |
3 (2.57) |
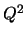 |
1 (2.71) |
4.0 (3.84) |
9 (6.63) |
|
Tabella:
Valori di 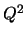 per calcolare le ellissi
che racchiudono le variabili
per calcolare le ellissi
che racchiudono le variabili  e
e  con probabilità
con probabilità 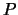 .
.
|
|
Le tabelle 9.4 e 9.5 forniscono alcuni
valori di interesse di 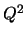 .
.
- L'angolo dell'asse maggiore dell'ellisse rispetto all'asse
delle ascisse è dato dalla relazione:
 |
(9.60) |
La figura 9.5 mostra
un esempio di distribuzione bivariata normale di parametri
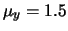 ,
,
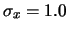 ,
,
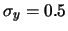 ,
,
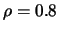 e
e 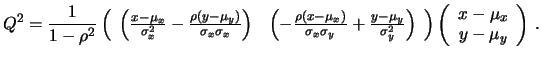 .
La distribuzione congiunta è rappresentata sia come
superficie nello spazio ( 9.5.a),
che densità di punti proporzionali
alla p.d.f. ( 9.5.d). Le funzioni di
densità di probabilità marginali
sono mostrate in 9.5.b e
9.5.c. Tre esempi di densità condizionate
cono mostrati in 9.5.d e 9.5.f,
per valori di
.
La distribuzione congiunta è rappresentata sia come
superficie nello spazio ( 9.5.a),
che densità di punti proporzionali
alla p.d.f. ( 9.5.d). Le funzioni di
densità di probabilità marginali
sono mostrate in 9.5.b e
9.5.c. Tre esempi di densità condizionate
cono mostrati in 9.5.d e 9.5.f,
per valori di  pari rispettivamente
a 1.25, 1.5 e 1.75. La Fig. 9.5.e
mostra infine le curve di equidensità
tali che la probabilità congiunta di
trovare i valori di
pari rispettivamente
a 1.25, 1.5 e 1.75. La Fig. 9.5.e
mostra infine le curve di equidensità
tali che la probabilità congiunta di
trovare i valori di  e di
e di 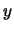 al loro interno
sia pari al 68 e al
al loro interno
sia pari al 68 e al 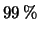 . Per confronto sono anche
riportati gli intervalli di probabilità al
. Per confronto sono anche
riportati gli intervalli di probabilità al 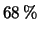 delle
distribuzioni marginali.
delle
distribuzioni marginali.




Next: pzd100 Caso generale di
Up: Variabili casuali multiple
Previous: pzd100 Distribuzione multinomiale
Indice
Giulio D'Agostini
2001-04-02
![]() e
e ![]() le variabili e
le variabili e
![]() ,
, ![]() ,
, ![]() e
e ![]() i parametri delle gaussiane
otteniamo
i parametri delle gaussiane
otteniamo
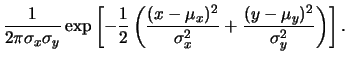
 ). In quest'ultimo caso infatti
ogni valore di
). In quest'ultimo caso infatti
ogni valore di 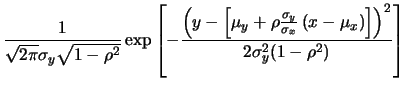 ).
).
![]() :
:
![]() descritta dalla (9.59)
è nota come la normale bivariata,
o binormale e la possiamo indicare con
descritta dalla (9.59)
è nota come la normale bivariata,
o binormale e la possiamo indicare con
![]() ,
,
 .
.
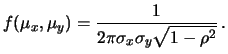 e vale
e vale
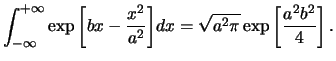
![]() ,
,
![]() ,
,
![]() ,
,
![]() e
e 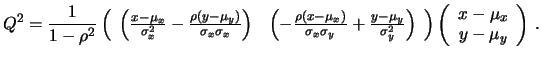 .
La distribuzione congiunta è rappresentata sia come
superficie nello spazio ( 9.5.a),
che densità di punti proporzionali
alla p.d.f. ( 9.5.d). Le funzioni di
densità di probabilità marginali
sono mostrate in 9.5.b e
9.5.c. Tre esempi di densità condizionate
cono mostrati in 9.5.d e 9.5.f,
per valori di
.
La distribuzione congiunta è rappresentata sia come
superficie nello spazio ( 9.5.a),
che densità di punti proporzionali
alla p.d.f. ( 9.5.d). Le funzioni di
densità di probabilità marginali
sono mostrate in 9.5.b e
9.5.c. Tre esempi di densità condizionate
cono mostrati in 9.5.d e 9.5.f,
per valori di ![]() pari rispettivamente
a 1.25, 1.5 e 1.75. La Fig. 9.5.e
mostra infine le curve di equidensità
tali che la probabilità congiunta di
trovare i valori di
pari rispettivamente
a 1.25, 1.5 e 1.75. La Fig. 9.5.e
mostra infine le curve di equidensità
tali che la probabilità congiunta di
trovare i valori di ![]() e di
e di ![]() al loro interno
sia pari al 68 e al
al loro interno
sia pari al 68 e al ![]() . Per confronto sono anche
riportati gli intervalli di probabilità al
. Per confronto sono anche
riportati gli intervalli di probabilità al ![]() delle
distribuzioni marginali.
delle
distribuzioni marginali.