



Next: Derivate di rispetto alle
Up: Variabili casuali multiple
Previous: pzd100Distribuzione normale bivariata
Indice
È semplice dimostrare che 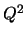 può essere riscritto
come il prodotto di un vettore riga per un vettore colonna
Il vettore riga può essere ulteriormente scomposto come
il prodotto di un vettore riga per una matrice
può essere riscritto
come il prodotto di un vettore riga per un vettore colonna
Il vettore riga può essere ulteriormente scomposto come
il prodotto di un vettore riga per una matrice 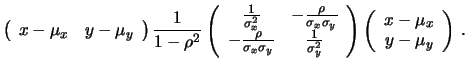 , ottenendo
così la seguente decomposizione:
, ottenendo
così la seguente decomposizione:
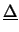 |
(9.61) |
Chiamando
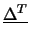 il vettore colonna della differenza
fra le variabili casuali e il loro valore atteso,
il vettore colonna della differenza
fra le variabili casuali e il loro valore atteso,
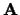 il vettore riga, in quanto trasposto di
il vettore riga, in quanto trasposto di
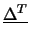 ,
e
,
e 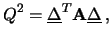 la matrice,
la matrice, 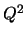 acquista la seguente forma:
con
acquista la seguente forma:
con
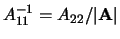 |
(9.62) |
È possibile riscrivere la matrice  in una forma più semplice
se si passa alla sua inversa9.7, ottenendo
in una forma più semplice
se si passa alla sua inversa9.7, ottenendo
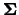 |
(9.63) |
La matrice
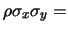 ha quindi un significato più immediato
di
ha quindi un significato più immediato
di 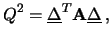 , in quanto i suoi elementi sono le varianze e le
covarianze delle variabili casuali
(si ricordi che
, in quanto i suoi elementi sono le varianze e le
covarianze delle variabili casuali
(si ricordi che
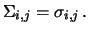 Cov
Cov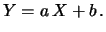 ). Utilizzando la
forma compatta
di scrivere le varianze
e covarianze per un
numero arbitrario di variabili casuali
(vedi par sec:covarianza)
si riconosce che
). Utilizzando la
forma compatta
di scrivere le varianze
e covarianze per un
numero arbitrario di variabili casuali
(vedi par sec:covarianza)
si riconosce che
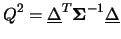 |
(9.64) |
Inoltre, si può dimostrare che l'espressione di 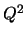 scritta
nella forma
scritta
nella forma
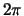 |
(9.65) |
può essere estesa ad un numero qualsiasi di variabili.
Questo ci permette di ottenere la formula generale della multinomiale,
se si riesce a scrivere in un modo compatto il denominatore
del termine di fronte
all'esponenziale. Per derivarne intuitivamente la forma si
pensi possono fare le seguenti considerazioni.
Poiché si può dimostrare che questa formula è valida
anche nel caso generale, abbiamo finalmente ottenuto l'espressione
della densità di probabilità di una distribuzione
multinomiale di  variabili comunque correlate fra di loro:
variabili comunque correlate fra di loro:
![$\displaystyle f(\underline{x}\,\vert\,{\cal N}(\underline{\mu}, {\bf\Sigma})) =...
... -\frac{1}{2}\underline{\Delta}^T{\bf\Sigma}^{-1}\underline{\Delta} \right]}\,,$](img2566.png) |
(9.66) |
ovvero
![$\displaystyle f(\underline{x}\,\vert\,{\cal N}(\underline{\mu}, {\bf\Sigma})) =...
...\underline{\mu})^T {\bf\Sigma}^{-1} (\underline{x}-\underline{\mu}) \right]}\,,$](img2567.png) |
(9.67) |
dove, ripetiamo ancora una volta,
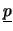 rappresenta
il vettore aleatorio
rappresenta
il vettore aleatorio
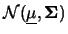 .
La notazione
.
La notazione
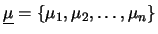 è simile a quella della semplice gaussiana, con le dovute
differenze:
è simile a quella della semplice gaussiana, con le dovute
differenze:
- al posto di una sola media
 ne abbiamo
ne abbiamo  , compattate in un vettore
, compattate in un vettore
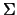 ;
;
- la deviazione standard è sostituita
da una matrice di varianze e covarianze
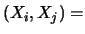 , chiamata
matrice di covarianza. Poiché vale che
Cov
, chiamata
matrice di covarianza. Poiché vale che
Cov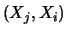 Cov
Cov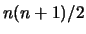 , la matrice è simmetrica
e i parametri indipendenti sono
, la matrice è simmetrica
e i parametri indipendenti sono 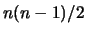 , ovvero
le
, ovvero
le  varianze e gli
varianze e gli 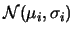 coefficienti di correlazione.
coefficienti di correlazione.
La densità di probabilità a molte dimensioni non è rappresentabile
graficamente. Si ricordi comunque che
- la distribuzione marginale di ciascuna delle variabili
 è una normale
è una normale
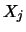 ;
;
- la distribuzione congiunta di due variabili qualsiasi
 e
e 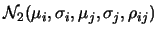 è una normale bivariata
è una normale bivariata
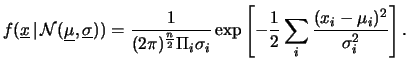 descritta dall'equazione ( 9.59).
descritta dall'equazione ( 9.59).
Si può verificare facilmente che, se i
coefficienti di correlazione fra le variabili sono tutti
nulli e quindi nella matrice di covarianza sono diversi da zero
soltanto i termini diagonali,
la ( 9.69)
si riduce al prodotto di  normali
univariate:
normali
univariate:
![$\displaystyle f(\underline{x}\,\vert\,{\cal N}(\underline{\mu}, \underline{\sig...
..._i} \exp{\left[ -\frac{1}{2} \sum_i\frac{(x_i-\mu_i)^2}{\sigma_i^2} \right]}\,.$](img2579.png) |
(9.68) |
Subsections




Next: Derivate di rispetto alle
Up: Variabili casuali multiple
Previous: pzd100Distribuzione normale bivariata
Indice
Giulio D'Agostini
2001-04-02
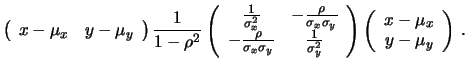 , ottenendo
così la seguente decomposizione:
, ottenendo
così la seguente decomposizione:
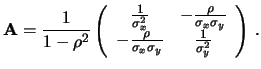
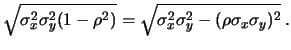 in forma compatta
estendibile ad un numero qualsiasi di variabili
riscriviamola come
in forma compatta
estendibile ad un numero qualsiasi di variabili
riscriviamola come
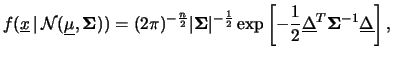 .
.
![$\displaystyle f(\underline{x}\,\vert\,{\cal N}(\underline{\mu}, {\bf\Sigma})) =...
... -\frac{1}{2}\underline{\Delta}^T{\bf\Sigma}^{-1}\underline{\Delta} \right]}\,,$](img2566.png)
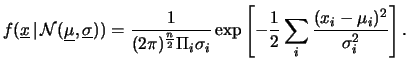 descritta dall'equazione ( 9.59).
descritta dall'equazione ( 9.59).