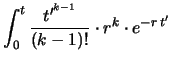Next: Previsione di una media
Up: Valore atteso e varianza
Previous: Valore atteso e varianza
Indice
Valore atteso e varianza della distribuzione
di Erlang
Anche il valore atteso e la previsione
del tempo in cui
si verifichi il  -mo successo in un processo di Poisson
(distribuzione di Erlang)
può essere valutato dalla proprietà delle combinazioni lineari di
variabili casuali indipendenti. Poiché il tempo di attesa
fra un evento e l'altro segue una distribuzione di esponenziale,
il tempo di attesa di
-mo successo in un processo di Poisson
(distribuzione di Erlang)
può essere valutato dalla proprietà delle combinazioni lineari di
variabili casuali indipendenti. Poiché il tempo di attesa
fra un evento e l'altro segue una distribuzione di esponenziale,
il tempo di attesa di  successi è pari alla somma di
successi è pari alla somma di
 variabili casuali ciascuna di valore atteso
e deviazione standard pari
variabili casuali ciascuna di valore atteso
e deviazione standard pari 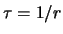 . Ne segue che
. Ne segue che
E Erlang Erlang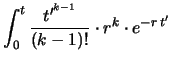 |
 |
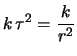 |
(10.38) |
Var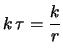 Erlang Erlang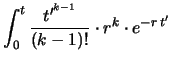 |
 |
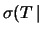 |
(10.39) |
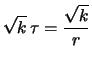 Erlang Erlang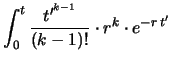 |
 |
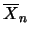 |
(10.40) |
Giulio D'Agostini
2001-04-02
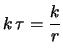 Erlang
Erlang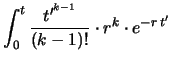
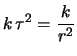
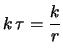 Erlang
Erlang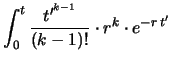
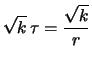 Erlang
Erlang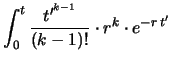
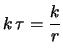 Erlang
Erlang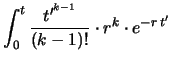
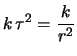
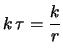 Erlang
Erlang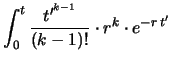
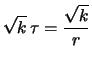 Erlang
Erlang